题目内容
【题目】选修4-5:不等式选讲
已知不等式![]()
![]() 的对任意实数
的对任意实数![]() 恒成立.
恒成立.
(Ⅰ)求实数![]() 的最小值
的最小值![]() ;
;
(Ⅱ)若![]() ,且满足
,且满足![]() ,求证:
,求证:![]() .
.
【答案】见解析
【解析】(Ⅰ)不等式![]() 等价于
等价于![]() .……………1分
.……………1分
令![]() ,则不等式
,则不等式![]()
![]() 的对任意实数
的对任意实数![]() 恒成立等价于
恒成立等价于![]() .………………2分
.………………2分
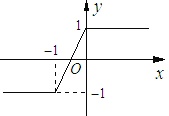
而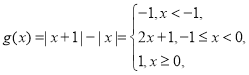 作出函数
作出函数![]() 的图象,由图可知,函数
的图象,由图可知,函数![]() 的最小值为
的最小值为![]() ,所以
,所以![]() ,即
,即![]() ,故
,故![]() .……………5分
.……………5分
(II)由(I)知![]() ,其中
,其中![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以原不等式等价于![]()
![]() .……………6分
.……………6分
下面证明不等式![]() :
:
因为![]() ,(当且仅当
,(当且仅当![]() 时取等号)
时取等号)
![]() , (当且仅当
, (当且仅当![]() 时取等号)
时取等号)
![]() .(当且仅当
.(当且仅当![]() 时取等号)……………8分
时取等号)……………8分
三式相加得:![]() ,(当且仅当
,(当且仅当![]() 时取等号)
时取等号)
……………9分
所以![]() ,即
,即![]() .………10分
.………10分
【命题意图】本题考查含有绝对值不等式的不等式恒成立问题、不等式的证明、函数图象的应用,意在考查推理论证能力、运算求解能力.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目