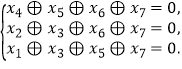题目内容
【题目】设a,b,c,d均为正数,且a+b=c+d,证明:
(1)若ab![]() cd,则
cd,则![]() +
+![]()
![]()
![]() +
+![]() ;
;
(2)![]() +
+![]()
![]()
![]() +
+![]() 是|a-b|
是|a-b|![]() |c-d|的充要条件
|c-d|的充要条件
【答案】
(1)
∵(![]() +
+![]() )2 =a+b+2
)2 =a+b+2![]() ,(
,(![]() +
+![]() )2=c+d+2
)2=c+d+2![]() ,
,
由题设a+b=c+d,ab![]() cd,得
cd,得![]() +
+![]() )2
)2![]() (
(![]() +
+![]() )2,
)2,
∴![]() +
+![]()
![]()
![]() +
+![]() 。
。
(2)
若|a-b|![]() |c-d|,则(a-b)2
|c-d|,则(a-b)2![]() (c-d)2,即(a+b)2-4ab
(c-d)2,即(a+b)2-4ab![]() (c+d)2-4cd
(c+d)2-4cd
∵a+b=c+d,
∴ab![]() cd,
cd,
由(I)得![]() +
+![]()
![]()
![]() +
+![]() 。
。
若![]() +
+![]()
![]()
![]() +
+![]() ,则(
,则(![]() +
+![]() )2
)2![]() (
(![]() +
+![]() )2,即a+b+2
)2,即a+b+2![]()
![]() c+d+2
c+d+2![]()
∵a+b=c+d,所以ab![]() cd,于是(a-b)2=(a+b)2-4ab
cd,于是(a-b)2=(a+b)2-4ab![]() (c+d)2-4cd=(c-d)2.
(c+d)2-4cd=(c-d)2.
∴|a-b|![]() |c-d|
|c-d|
综上所述,![]() +
+![]()
![]()
![]() +
+![]() 是|a-b|
是|a-b|![]() |c-d|的充要条件。
|c-d|的充要条件。
【解析】(I)要证明![]() +
+![]()
![]()
![]() +
+![]() , 只需证明(
, 只需证明(![]() +
+![]() )2
)2![]() (
(![]() +
+![]() )2;展开结合已知条件易证;
)2;展开结合已知条件易证;
(Ⅱ)充要条件的证明需要分为两步,即充分条件的证明和必要条件的证明.证明的关键是寻找条件和结论以及它们和已知之间的联系.
【考点精析】解答此题的关键在于理解归纳推理的相关知识,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理,以及对类比推理的理解,了解根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另外一类事物类似的性质的推理,叫做类比推理.

【题目】![]() 某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图
某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图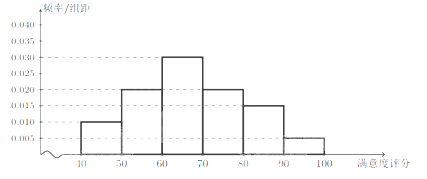
B地区用户满意度评分的频率分布表
满意度评分分组 | [50,60) | [50,60) | [50,60) | [50,60) | [50,60) |
频数 | 2 | 8 | 14 | 10 | 6 |
(1)(I)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分 散 程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图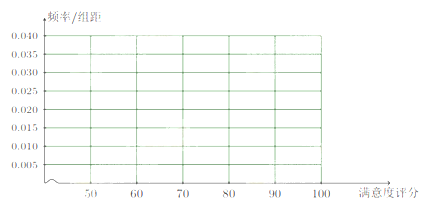
(2)(II)根据用户满意度评分,将用户的满意度评分分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
【题目】(2015·新课标I卷)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi=1;2…8数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中wi=![]() ,
,![]() =
=![]()
(1)根据散点图判断,y=a+bx与y=c+d![]() ,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(2)根据(I)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x , y的关系为z=0.2y-x,根据(II)的结果回答下列问题:
(i)当年宣传费x=90时,年销售量及年利润的预报值时多少?
(ii)当年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),……,(un,vn),其回归线v=![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: