题目内容
【题目】(2015·新课标I卷)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi=1;2…8数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中wi=![]() ,
,![]() =
=![]()
(1)根据散点图判断,y=a+bx与y=c+d![]() ,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(2)根据(I)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x , y的关系为z=0.2y-x,根据(II)的结果回答下列问题:
(i)当年宣传费x=90时,年销售量及年利润的预报值时多少?
(ii)当年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),……,(un,vn),其回归线v=![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
【答案】
(1)
y=c+d![]() 适合作为年销售y关于年宣传费用x的回归方程类型。
适合作为年销售y关于年宣传费用x的回归方程类型。
(2)
![]() =100.6+68
=100.6+68![]()
(3)
46.24
【解析】(I)由散点图及所给函数图像即可选出适合作为拟合的函数;(II)令w=![]() ,先求出建立y关于w的线性回归方程,即可y关于x的回归方程;(III) : (i) 利用y关于x的回归方程先求出年销售量y预报值,再根据年利率z与x,y的关系为z=0.2y-x即可年利润z的预报值,(ii) 根据(II)的结果知,
,先求出建立y关于w的线性回归方程,即可y关于x的回归方程;(III) : (i) 利用y关于x的回归方程先求出年销售量y预报值,再根据年利率z与x,y的关系为z=0.2y-x即可年利润z的预报值,(ii) 根据(II)的结果知,
利润z的预报值,列出关于x的方程,利用二次函数求最值的方法即可求出年利润取最大值时的年宣传费用.
试题解析:(I)由散点图可以判断,y=c+d![]() 适合作为年销售y关于年宣传费用x的回归方程类型。
适合作为年销售y关于年宣传费用x的回归方程类型。
(II)令w=![]() ,先建立y关于w的线性回归方程,由于
,先建立y关于w的线性回归方程,由于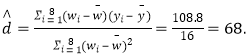
![]()
∴![]()
∴y关于w的线性回归方程为![]() =100.6+68w, ∴y关于x的回归方程为
=100.6+68w, ∴y关于x的回归方程为![]() =100.6+68
=100.6+68![]() .
.
(III)(i)由(II)知,当x=49时,年销量y的预报值,![]() =100.6+68
=100.6+68![]() =576.6,
=576.6,![]() =576.6x0.2-49=66.32 (ii)根据(II)的结果知,年利润z的预报值
=576.6x0.2-49=66.32 (ii)根据(II)的结果知,年利润z的预报值![]() =0.2(100.6+68
=0.2(100.6+68![]() )-x=-x+13.6
)-x=-x+13.6![]() +20.12,∴ 当
+20.12,∴ 当![]() =
=![]() =6.8,即x=46.24时,
=6.8,即x=46.24时,![]() 取得最大值。
取得最大值。
【分 析】本题考查了非线性拟合及非线性回归方程的求解与应用,是源于课本的试题类型,解答非线性拟合问题,先作出散点图,再根据散点图选择合适的函数类型,设 出回归方程,利用换元法将非线性回归方程化为线性回归方程,求出样本数据换元后的值,然后根据线性回归方程的计算方法计算变换后的线性回归方程系数,即可 求出非线性回归方程,再利用回归方程进行预报预测,注意计算要细心,避免计算错误.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案【题目】![]() 某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度平分如下:
某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度平分如下:
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(1)(I)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可)
(2)(II)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
|
|
|
|
|
|
|
|
记时间C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立。根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
(1)从该班随机选1名同学,求该同学至少参加一个社团的概率;
(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1 , A2 , A3 , A4 , A5 , 3名女同学B1 , B2 , B3 . 现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.


