题目内容
10.如图:长方体ABCD-A1B1C1D1,AB=12,BB1=5,则直线B1C1到平面A1BCD1的距离$\frac{60}{13}$.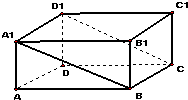
分析 欲求直线B1C1和平面A1BCD1的距离,结合长方体,将原距离转化为点B1和平面A1B的距离解决,最终转化为直角三角形斜边上的高求解即可.
解答 解:直线B1C1和平面A1BCD1的距离即为点B1和平面A1B的距离.
即为直角三角形A1BB1斜边上的高d,
由面积法得:d=$\frac{5×12}{13}$=$\frac{60}{13}$.
故答案为:$\frac{60}{13}$.
点评 本题主要考查了点、线、面间的距离计算,以及空间几何体的概念、空间想象力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设集合A={x|2<x<5},B={x|x<b},若A⊆B,则b的取值范围是( )
| A. | b≤2 | B. | b≤5 | C. | b≥2 | D. | b≥5 |
5.△ABC中,三个角A,B,C所对的边a,b,c满足a2+b2=c2-$\sqrt{3}$ab,则C=( )
| A. | 150° | B. | 135° | C. | 120° | D. | 60° |
15.直线2x-y-10=0和圆(x-2)2+(y+1)2=3的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交但不过圆心 | D. | 过圆心 |
19.已知直线x=m与函数f(x)=sinx,函数g(x)=sin($\frac{π}{2}$-x)的图象分别相交于M、N两点,则|MN|的最大值为( )
| A. | 1 | B. | $\sqrt{2}-1$ | C. | $\sqrt{2}$ | D. | 2 |