Question

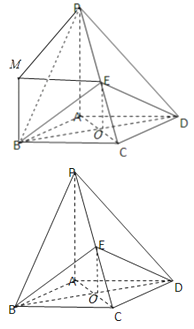
【题目】如图4，四边形ABCD为菱形，∠ABC=60°．PA⊥平面ABCD，E为PC中点．
（Ⅰ）求证：平面BED⊥平面ABCD；
（Ⅱ）求平面PBA与平面EBD所成二面角（锐角）的余弦值．

Answer 1

【答案】证明：（Ⅰ）连结AC交BD于点O，连结OE，则O是AC的中点．
又知E是AP中点
∴EO∥PC，
∵PC⊥平面ABCD，∴OE⊥平面ABCD．
又知OE平面BDE，
∴平面EBD⊥平面ABCD．
（Ⅱ）解：过B作BM⊥平面ABCD，连结PM，ME，如图，
由（Ⅰ）可知，PA∥EO∥MB，
则MB是平面PBA与平面EBD的交线，可得MB⊥AB，MB⊥BO，
∠ABO计算平面PBA与平面EBD所成二面角的平面角，
四边形ABCD为菱形，∠ABC=60°．可知：∠ABO=30°
cos∠ABO=cos30°=．
平面PBA与平面EBD所成二面角（锐角）的余弦值：．

【解析】（Ⅰ）证明面面垂直一般利用面面垂直的判定定理故可连接EO可利用中位线定理证得EO∥PC再结合PC⊥平面ABCD可得EO⊥平面ABCD即可得证．
（Ⅱ）过B作BM⊥平面ABCD，连结PM，ME，说明∠ABO计算平面PBA与平面EBD所成二面角的平面角，利用已知条件求出角的大小，即可求解余弦值．
【考点精析】通过灵活运用平面与平面垂直的判定，掌握一个平面过另一个平面的垂线，则这两个平面垂直即可以解答此题．