Question

【题目】在三棱锥S-ABC中，已知SC⊥平面ABC，AB=BC=CA，SC=2，D、E分别为AB、BC的中点.若点P在SE上移动，求△PCD面积的最小值.

Answer 1

【答案】

【解析】

如图，在三棱锥S-ABC中，底面ABC为正三角形，D为AB的中点.

则 .

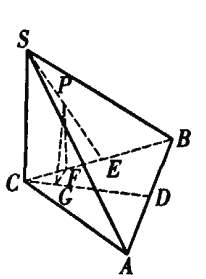
于是，要求△PCD面积的最小值，只需求点P到直线CD距离的最小值.

在平面SBC内过点P作PF⊥BC，垂足为F.

因为SC⊥面ABC，所以，面ABC⊥面SBC，交线为BC.

由面与面垂直的性质定理知PF ⊥平面AB.

过点F在平面ABC内作FG⊥CD，垂足为G，联结PG.

则由三垂线定理知CD⊥PG.

于是，点P到CD的距离为PG.

设PF=x.由SC=2，则（0，2）.

易知，Rt△SCE∽Rt△PFE.

故

在Rt△FGC中,FG=CF,sin∠FCG

在Rt△FGP中，

于是，当号时，PG取最小值.3故△PCD面积的最小值为.