题目内容
已知函数
 .
.
(1)求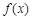 的单调区间;
的单调区间;
(2)设 ,若对任意
,若对任意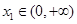 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
(1) 函数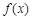 的单调递增区间为
的单调递增区间为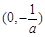 ,单调递减区间为
,单调递减区间为
(2)
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知函数
 .
.
(1)求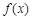 的单调区间;
的单调区间;
(2)设 ,若对任意
,若对任意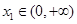 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
(1) 函数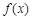 的单调递增区间为
的单调递增区间为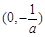 ,单调递减区间为
,单调递减区间为
(2)
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案