题目内容
(本小题满分14分)设函数 ,
, .
.
(Ⅰ)当 时,
时, 在
在 上恒成立,求实数
上恒成立,求实数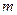 的取值范围;
的取值范围;
(Ⅱ)当 时,若函数
时,若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 的取值
的取值 范围;
范围;
(Ⅲ)是否存在实数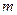 ,使函数
,使函数 和函数
和函数 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出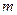 的值,若不存在,说明理由.
的值,若不存在,说明理由.
解:(Ⅰ)由 a=0,f(x)≥h(x)可得-mlnx≥-x 即
a=0,f(x)≥h(x)可得-mlnx≥-x 即 ┉┉┉┉┉┉┉┉1分
┉┉┉┉┉┉┉┉1分
记 ,则f(x)≥h(x)在(1,+∞)上恒成立等价于
,则f(x)≥h(x)在(1,+∞)上恒成立等价于 .
.
求得 ┉┉┉┉┉┉┉┉2分
┉┉┉┉┉┉┉┉2分
当 时;
时; ;当
;当 时,
时, ┉┉┉┉┉┉┉┉3分
┉┉┉┉┉┉┉┉3分
故 在x=e处取得极小值,也是最小值,
在x=e处取得极小值,也是最小值,
即 ,故
,故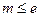 . ┉┉┉┉┉┉┉┉4分
. ┉┉┉┉┉┉┉┉4分
(Ⅱ)函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同的零点等价于方程x-2lnx=a,在[1,3]上恰有两个相异实根。┉┉┉┉┉┉┉┉5分
令g(x)=x-2lnx,则 ┉┉┉┉┉┉┉┉6分
┉┉┉┉┉┉┉┉6分
当 时,
时, ,当
,当 时,
时,
g(x)在[1,2]上是单调递减函数,在 上是单调递增函数。
上是单调递增函数。
故 ┉┉┉┉┉┉┉┉8分
┉┉┉┉┉┉┉┉8分
又g(1)=1,g(3)=3-2ln3
∵g(1)>g(3),∴只需g(2) <a≤g(3),
<a≤g(3),
故a的取值范围是(2-2ln2,3-2ln3) ┉┉┉┉┉┉┉┉9分
(Ⅲ)存在m= ,使得函数f(x)和函数h(x)在公共定
,使得函数f(x)和函数h(x)在公共定 义域上具有相同的单调性
义域上具有相同的单调性 ,函数f(x)的定义域为(0,+∞)。┉┉┉┉┉┉10分
,函数f(x)的定义域为(0,+∞)。┉┉┉┉┉┉10分
若 ,则
,则
 ,函数f(x)在(0,+
,函数f(x)在(0,+ ∞)上单调递增,不合题意;┉┉┉11分
∞)上单调递增,不合题意;┉┉┉11分
若 ,由
,由 可得2x2-m>0,解得x>
可得2x2-m>0,解得x> 或x<-
或x<- (舍去)
(舍去)
故 时,函数的单调递增区间为(
时,函数的单调递增区间为( ,+∞)
,+∞)
单调递减区间为(0,  ) ┉┉┉┉┉┉┉┉12分
) ┉┉┉┉┉┉┉┉12分
而h(x)在(0,+∞)上的单调递减区间是(0, ),单调递增区间是(
),单调递增区间是( ,+∞)
,+∞)
故只需 =
= ,解之得m=
,解之得m= ┉┉┉┉┉┉┉┉13分
┉┉┉┉┉┉┉┉13分
即当m= 时,函数f(x)和函数h(x)在其公共定义域上具有相同的单调性。┉14分.
时,函数f(x)和函数h(x)在其公共定义域上具有相同的单调性。┉14分.
解析


 .
.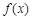 的单调区间;
的单调区间; ,若对任意
,若对任意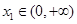 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围. .
. 在
在 上的最小值;
上的最小值; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
, .
. 的单调区间和最小值;
的单调区间和最小值; 的大小关系;
的大小关系;
 的取值范围,使得
的取值范围,使得 <
< 对任意
对任意 >0成立
>0成立 ,其中
,其中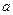 为常数.
为常数. ,
, 的图象恒过定点;
的图象恒过定点; 时,判断函数
时,判断函数 时,
时, 的最大值.
的最大值. .
. ,
,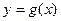 在
在 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程; 单调递增,求
单调递增,求 的取值范围.
的取值范围. 过点
过点 ,且与曲线
,且与曲线 和
和 都相切,
都相切, 的值。
的值。 .
. ,讨论
,讨论 的单调性;
的单调性; 恒有
恒有 ,求
,求 的取值范围.
的取值范围. 的一个极值点
的一个极值点 ,试问过点(2,5)可作多少条直线与曲线
,试问过点(2,5)可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由.