题目内容
在直三棱柱 中,
中, ,
, ,求:
,求:
(1)异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)直线 到平面
到平面 的距离.
的距离.
(1) 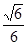 .(2)
.(2) 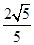
解析试题分析:(1)将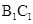 平移到
平移到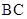 ,根据异面直线所成角的定义可知
,根据异面直线所成角的定义可知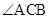 为异面直线
为异面直线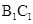 与
与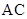 所成角(或它的补角),在
所成角(或它的补角),在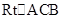 中求出此角即可;
中求出此角即可;
(2)根据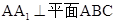 ,则
,则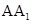 就是几何体的高,再求出底面积,最后根据三棱锥
就是几何体的高,再求出底面积,最后根据三棱锥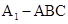 的体积公式
的体积公式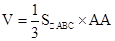 求解.
求解.
试题解析:(1)因为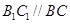 ,所以
,所以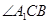 (或其补角)是异面直线
(或其补角)是异面直线 与
与 所成角. 1分
所成角. 1分
因为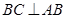 ,
,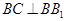 ,所以
,所以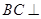 平面
平面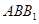 ,所以
,所以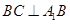 . 3分
. 3分
在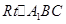 中,
中, , 5分
, 5分
所以异面直线 与
与 所成角的余弦值为
所成角的余弦值为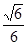 . 6分
. 6分
(2)因为 //平面
//平面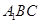
所以 到平面
到平面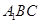 的距离等于
的距离等于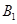 到平面
到平面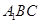 的距离 8分
的距离 8分
设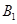 到平面
到平面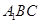 的距离为
的距离为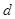 ,
,
因为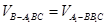 ,所以
,所以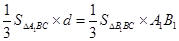 10分
10分
可得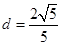 11分
11分
直线 与平面
与平面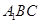 的距离为
的距离为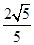 . 12分
. 12分
考点:两条异面直线所成角的余弦值; 直线到平面的距离

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是直棱柱,
是直棱柱, .点
.点 分别为
分别为 和
和 的中点.
的中点. 
 平面
平面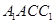 ;
; 到平面
到平面 的距离.
的距离. 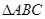 在平面
在平面 内,
内, ,
, ,P为平面
,P为平面 ,
,


 的面积取得最大值时,求直线BC与平面PAB所成角的大小
的面积取得最大值时,求直线BC与平面PAB所成角的大小 ,边长为
,边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
 平面PAD.
平面PAD. 的底面边长是
的底面边长是 ,侧棱长是
,侧棱长是 ,
, 是
是 的中点.
的中点.
 ∥平面
∥平面 ;
; 的大小;
的大小; 上是否存在一点
上是否存在一点 ,使得平面
,使得平面
 平面
平面 的长;若不存在,说明理由.
的长;若不存在,说明理由. ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.


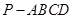 中,
中,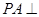 面
面 ,
,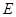 、
、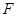 分别为
分别为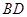 、
、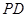 的中点,
的中点,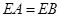 .
.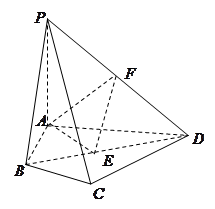
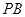 ∥面
∥面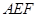 ;
;