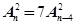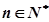题目内容
三位老师和三位学生站成一排,要求任何两位学生都不相邻,则不同的排法总数为( )
| A.720 | B.144 | C.36 | D.12 |
B
解:∵要求任何两位学生不站在一起,
∴可以采用插空法,
先排3位老师,有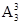 种结果,
种结果,
再使三位学生在教师形成的4个空上排列,有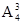 种结果,
种结果,
根据分步计数原理知共有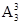
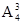 =144种结果,
=144种结果,
故选B
∴可以采用插空法,
先排3位老师,有
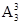 种结果,
种结果,再使三位学生在教师形成的4个空上排列,有
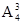 种结果,
种结果,根据分步计数原理知共有
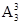
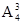 =144种结果,
=144种结果,故选B

练习册系列答案
相关题目
 的展开式中,前三项的系数成等差数列.
的展开式中,前三项的系数成等差数列.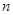 ;
;