Question

【题目】在数列{an}中， （c为常数，n∈N*），且a1 ， a2 ， a5成公比不为1的等比数列． （Ⅰ）求证：数列 是等差数列；
（Ⅱ）求c的值；
（Ⅲ）设bn=anan+1 ， 求数列{bn}的前n项和Sn ．

Answer 1

【答案】解：（Ⅰ）因为 ，所以an≠0， 则 ，又c为常数，
∴数列 是等差数列；
（Ⅱ）由（Ⅰ）可知 ，
∵a1=1，∴a2= ，a5= ，
∵a1 ， a2 ， a5成公比不为1的等比数列，所以 ，
解得c=0或c=2，当c=0时，an=an+1 ， 不满足题意，舍去，
所以c的值为2；
（Ⅲ）由（Ⅱ）可知c=2，∴ ，
bn=anan+1= = ，
所以数列{bn}的前n项和
Sn= =
【解析】（Ⅰ）通过已知条件，方程去倒数，即可推出数列满足等差数列的定义，说明数列 是等差数列；（Ⅱ）通过第一问，直接求出a1 ， a2 ， a5 ， 利用等比数列直接求出c的值；（Ⅲ）通过第二问，求出an ， 然后利用bn=anan+1 ， 通过裂项法直接求数列{bn}的前n项和Sn ．
【考点精析】通过灵活运用数列的前n项和，掌握数列{an}的前n项和sn与通项an的关系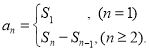即可以解答此题．