题目内容
【题目】[选修4-5：不等式选讲]
已知函数f（x）=|x+b2|﹣|﹣x+1|，g（x）=|x+a2+c2|+|x﹣2b2|，其中a，b，c均为正实数，且ab+bc+ac=1．
（Ⅰ）当b=1时，求不等式f（x）≥1的解集；
（Ⅱ）当x∈R时，求证f（x）≤g（x）．
【答案】解：（Ⅰ）由题意，当b=1时，f（x）=|x+b2|﹣|﹣x+1|=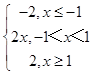 
， 当x≤﹣1时，f（x）=﹣2＜1，不等式f（x）≥1无解，不等式f（x）≥1的解集为；
当﹣1＜x＜1时，f（x）=2x，由不等式f（x）≥1，解得x≥ 
，所以 ≤x＜1；
当x≥1时，f（x）=2≥1恒成立，
所以不等式f（x）≥1的解集为[ ，+∞）．
（Ⅱ）（Ⅱ）当x∈R时，f（x）=|x+b2|﹣|﹣x+1|≤|x+b2 +（﹣x+1）|=|b2+1|=b2+1；
g（x）=|x+a2+c2|+|x﹣2b2|=≥|x+a2+c2﹣（x﹣2b2）|=|a2+c2+2b2|=a2+c2+2b2 ．
而 a2+c2+2b2﹣（b2+1）=a2+c2+b2﹣1= （ a2+c2+b2+a2+c2+b2 ）﹣1≥ab+bc+ac﹣1=0，
当且仅当a=b=c= 
时，等号成立，即 a2+c2+2b2≥b2+1，即f（x）≤g（x）．
【解析】（Ⅰ）当b=1时，把f（x）用分段函数来表示，分类讨论，求得f（x）≥1的解集．（Ⅱ）当x∈R时，先求得f（x）的最大值为b2+1，再求得g（x）的最小值，根据g（x）的最小值减去f（x）的最大值大于或等于零，可得f（x）≤g（x）成立．
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识，掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．
