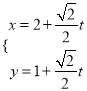ƒøƒ⁄»ð
°æƒø°øæðÕ≥º∆£¨Ωÿ÷¡2016ƒÍµ◊»´π˙Œ¢–≈◊¢≤·”√ªß ˝¡ø“—æ≠Õª∆∆9.27“⁄.Œ™µ˜≤È¥Û—ß…˙’‚∏ˆŒ¢–≈”√ªß»∫ÃÂ÷–√ø»À”µ”–Œ¢–≈»∫µƒ ˝¡ø£¨œ÷¥”ƒ≥ –¥Û—ß…˙÷–Àʪ˙≥È»°100ŒªÕ¨—ßΩ¯––¡À≥È—˘µ˜≤È£¨Ω·π˚»Áœ¬£∫
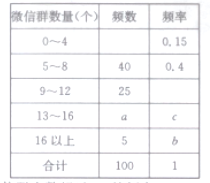
£®1£©«Û![]() £¨
£¨![]() £¨
£¨![]() µƒ÷µº∞—˘±æ÷–Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ £ª
µƒ÷µº∞—˘±æ÷–Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ £ª
£®2£©»Ù¥”’‚100ŒªÕ¨—ß÷–Àʪ˙≥È»°2»À£¨«Û’‚2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ £ª
£®3£©“‘£®1£©÷–µƒ∆µ¬ ◊˜Œ™∏≈¬ £¨»Ù¥”»´ –¥Û—ß…˙÷–Àʪ˙≥È»°3»À£¨º«![]() ±Ì æ≥ÈµΩµƒ «Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ»À ˝£¨«Û
±Ì æ≥ÈµΩµƒ «Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ»À ˝£¨«Û![]() µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚
µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚![]() .
.
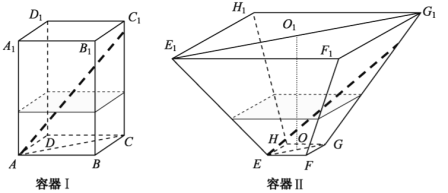
°æ¥∞∏°ø£®1£©![]() .£®2£©
.£®2£©![]() .£®3£©º˚Ω‚Œˆ
.£®3£©º˚Ω‚Œˆ
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫
(1)¿˚”√∆µ¬ ∑÷≤º±Ìø…µ√![]() £¨
£¨![]() £¨
£¨![]() .‘ÚŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™
.‘ÚŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™![]() .
.
(2)”…“‚ø…µ√2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ Œ™![]() .
.
(3)”…“‚ø…µ√![]() µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.Ω·∫œ∏≈¬ π´ Ω∫Õ∂˛œÓ∑÷≤ºµƒπ´ Ωº¥ø…«Ûµ√∑÷≤º¡–£¨»ª∫Û«ÛΩ‚ ˝—ß∆⁄Õ˚ø…µ√
µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.Ω·∫œ∏≈¬ π´ Ω∫Õ∂˛œÓ∑÷≤ºµƒπ´ Ωº¥ø…«Ûµ√∑÷≤º¡–£¨»ª∫Û«ÛΩ‚ ˝—ß∆⁄Õ˚ø…µ√![]() .
.
‘Ã‚Ω‚Œˆ£∫
£®1£©‘⁄0÷¡4∏ˆ’‚“ª∂Œ£¨∂‘”¶µƒ∆µ ˝Œ™15£¨
”…“—÷™µ√£∫![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý![]() £¨
£¨![]() .Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™
.Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∆µ¬ Œ™![]() .
.
£®2£©º«°∞2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12°±Œ™ ¬º˛![]() £¨‘Ú
£¨‘Ú![]() .
.
À˘“‘£¨2»À÷–«°”–1»ÀŒ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ Œ™![]() .
.
£®3£©“¿Ã‚“‚ø…÷™£¨Œ¢–≈»∫∏ˆ ˝≥¨π˝12µƒ∏≈¬ Œ™![]() .
.
![]() µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.
µƒÀ˘”–ø…ƒÐ»°÷µ0£¨1£¨2£¨3.
‘Ú![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() .
.
∆‰∑÷≤º¡–»Áœ¬£∫
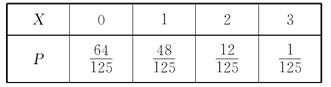
À˘“‘£¨![]()
![]() £¨ªÚ
£¨ªÚ![]() .
.

 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏