题目内容
【题目】选修4-4：坐标系与参数方程
以坐标原点
为极点，以
轴正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，直线
的参数方程为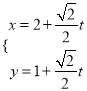
（
为参数），圆
的极坐标方程为
.
（1）求直线
的普通方程与圆
的直角坐标方程；
（2）设圆
与直线
交于
两点，若点
的直角坐标为
，求
的值.
【答案】（1）l的方程为： 
，圆
的方程为： 
;（2）
.
【解析】试题分析：（1）直线
的参数方程为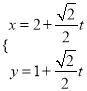
，消去
，求得普通方程： 
，由
，可得： 
，即可求得
圆
的直角坐标系；
（2）将参数方程代入曲线圆
的直角坐标系，可求得
由韦达定理可知
即
2异号，可知
试题解析：（1）直线的普通方程为： 
，
，所以
，
所以曲线
的直角坐标方程为： 
.
（2）点
在直线
上，且在圆
内，把
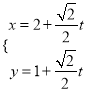代入
得
，设两个实根为
，则
，即
异号，所以
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某工厂为了对研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
（1）求回归直线方程
；
（2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是5元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润
销售收入
成本）（附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为：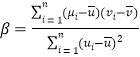
，
），
，
