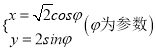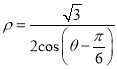题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,过椭圆的左焦点
,过椭圆的左焦点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相交所得弦的长度为1.
相交所得弦的长度为1.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() ,设
,设![]() ,
, ![]() ,其中
,其中![]() 为坐标原点.当以线段
为坐标原点.当以线段![]() 为直径的圆恰好过点
为直径的圆恰好过点![]() 时,求证:
时,求证: ![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
【答案】(1)![]() ;(2)定值为
;(2)定值为![]() ,证明见解析.
,证明见解析.
【解析】试题分析:(I)借助题设条件建立方程组求解;(II)依据题设运用直线与椭圆的位置关系进行探求.
试题解析:
(Ⅰ)由题意知![]() 得
得![]() ,即
,即![]() . ①
. ①
因为直线过左焦点![]() 且倾斜角为30°可得直线方程为
且倾斜角为30°可得直线方程为![]()
又因为直线![]() 与圆
与圆![]() 相交弦长为1,
相交弦长为1,
所以圆心到直线距离![]() ,
,
再由勾股定理得:![]() ②
②
由①②联立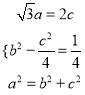 可知
可知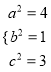
即椭圆方程为![]()
(Ⅱ)(ⅰ)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,因为以线段
,因为以线段![]() 为直径的圆过原点,所以
为直径的圆过原点,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() ,③
,③
又因为点![]() 在椭圆上,所以
在椭圆上,所以![]() ,④
,④
把③代入④得: ![]() ,
,
所以![]() .
.
(ⅱ)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
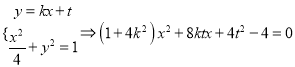 ,
,
因为交于不同两点,所以![]() ,
,
![]() ,即
,即![]() ,
,
由韦达定理得: ![]() ,
,
由题意知![]() 即
即![]() ,又
,又![]() ,
,
所以![]() ,
,
∴![]() ,
,
代入整理得![]() .⑤
.⑤
又![]()
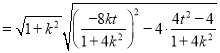
![]()
点![]() 到直线
到直线![]() 的距离
的距离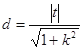 ,
,
所以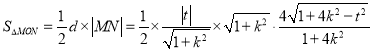
![]() ,⑥
,⑥
将⑤代入⑥得![]() ,
,
综上,三角形![]() 的面积为定值1.
的面积为定值1.

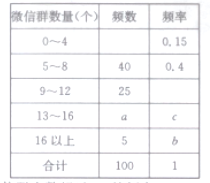
【题目】共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
使用时间 |
|
|
|
|
|
人数 | 10 | 40 | 25 | 20 | 5 |
(Ⅰ)已知该校大一学生由2400人,求抽取的100名学生中大一学生人数;
(Ⅱ)作出这些数据的频率分布直方图;
(Ⅲ)估计该校大学生每周使用共享单车的平均时间![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用![]() 、
、![]() 、
、![]() 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| 甲 | 4次 | 6次 | 2次 | 12次 |
| 乙 | 3次 | 6次 | 3次 | 12次 |
| 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只能是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.