题目内容
【题目】在平面直角坐标系xOy中,己知圆C经过点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),且与直线
),且与直线![]() 相切.
相切.
(1)求圆C的方程;
(2)设P是直线l:x=4上的任意一点,过点P作圆C的切线,切点为M,N.
①求证:直线MN过定点(记为Q);
②设直线PQ与圆C交于点A,B,与y轴交于点D.若![]() ,
,![]() ,求+的值.
,求+的值.
【答案】(1)![]() (2)①证明见解析;②
(2)①证明见解析;②![]()
【解析】
(1)设圆C的方程为![]() ,由此得
,由此得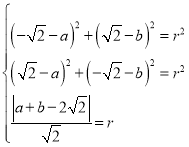 ,解出即可;
,解出即可;
(2)①设P(4,![]() ),由题意P,M,N,C在以PC为直径的圆
),由题意P,M,N,C在以PC为直径的圆![]() 上,两圆方程作差可得直线MN的方程为
上,两圆方程作差可得直线MN的方程为![]() ,由直线系方程即可求出定点;
,由直线系方程即可求出定点;
②由①得Q(1,0),设直线PQ的方程为![]() ,则D(0,﹣k),设A(
,则D(0,﹣k),设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),联立直线与圆的方程消元,由韦达定理可得
),联立直线与圆的方程消元,由韦达定理可得 ,根据题意可得到
,根据题意可得到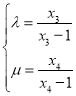 ,代入后化简求值即可.
,代入后化简求值即可.
解:(1)设圆C的方程为![]() ,
,
由题意可得,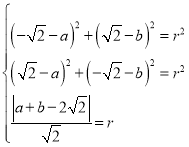 ,
,
解得![]() ,
,![]() ,
,![]() ,
,
∴圆C的方程为![]() ;
;
(2)①设P(4,![]() ),
),
∵PM,PN是圆C的两条切线,
∴PM⊥MC,PN⊥NC,
∴P,M,N,C在以PC为直径的圆上,
∴该圆上任意一点![]() 满足
满足![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴该圆方程为![]() ,
,
由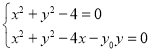 作差可得公共弦所在直线MN的方程为
作差可得公共弦所在直线MN的方程为![]() ,
,
∴直线MN过定点(1,0);
②由①可得Q(1,0),设直线PQ的方程为![]() ,则D(0,﹣k),
,则D(0,﹣k),
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
由![]() 得
得![]() ,
,
∴ ,
,
由![]() ,
,![]() ,得
,得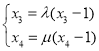 ,即
,即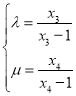 ,
,
∴![]()
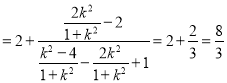 .
.

练习册系列答案
相关题目