题目内容
【题目】已知椭圆![]() 的右焦点为F,直线l与C交于M,N两点.
的右焦点为F,直线l与C交于M,N两点.
(1)若l过点F,点M,N到直线y=2的距离分别为d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若点M的坐标为(0,1),直线m过点M交C于另一点N′,当直线l与m的斜率之和为2时,证明:直线NN′过定点.
【答案】(1)x﹣y﹣1=0或x﹣2y﹣1=0(2)证明见解析;
【解析】
(1)由若l过椭圆的右焦点F(1,0),设直线l的方程为x=my+1,联立直线与椭圆方程,消去x,得交点M,N的纵坐标关系,因为点M,N到直线y=2的距离分别为d1,d2,则d1+d2=2﹣yM+2﹣yN=4﹣(yM+yN)![]() ,转化为m的方程,求得m即可.
,转化为m的方程,求得m即可.
(2)分类讨论,当直线NN'的斜率不存在和存在两种情况,设出直线方程,联立直线与椭圆的方程,消去一个变量,由韦达定理得出N,N'的坐标的关系式,再由当直线l与m的斜率之和为2,列出方程,求出直线方程,即可得直线NN'过定点(﹣1,﹣1).
(1)易知F(1,0),设直线l的方程为x=my+1,
由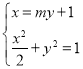 得(m2+2)y2+2my﹣1=0.则yM+yN
得(m2+2)y2+2my﹣1=0.则yM+yN![]() .
.
因为d1+d2=2﹣yM+2﹣yN=4﹣(yM+yN)=4![]() .
.
所以m=1或m=2.
故l的方程为x﹣y﹣1=0或x﹣2y﹣1=0.
(2)证明:当直线NN'的斜率不存在时,设N(x0,y0),则N'(x0,﹣y0).
由kl+km=2,得![]() 2,解得x0=﹣1.
2,解得x0=﹣1.
当直线NN'的斜率存在时,
设直线NN'的方程为y=kx+t(t≠1),N(x1,y1),N'(x2,y2).
由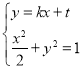 得(1+2k2)x2+4ktx+2t2﹣2=0.
得(1+2k2)x2+4ktx+2t2﹣2=0.
所以x1+x2![]() ,x1x2
,x1x2![]() ;
;
因为kl+km=2.
所以![]() 2k
2k![]() 2k
2k![]() 2k
2k![]() 2.
2.
所以t=k﹣1,所以直线NN'的方程为y=kx+k﹣1,即y+1=k(x+1).
故直线NN'过定点(﹣1,﹣1).
综上,直线NN'过定点(﹣1,﹣1).

 春雨教育同步作文系列答案
春雨教育同步作文系列答案