题目内容
15.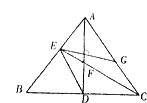 如图所示,在△ABC中,AD∩CE=F,AD⊥EG,且F为△ABC的内心.
如图所示,在△ABC中,AD∩CE=F,AD⊥EG,且F为△ABC的内心.(1)若B、D、F、E四点共圆,求∠B的大小;
(2)在(1)的条件下,求证:CE平分∠DEG.
分析 (1)利用F为△ABC的内心,可得∠AFE=$\frac{1}{2}$(∠A+∠C),利用B、D、F、E四点共圆,可得∠AFE=∠B=$\frac{1}{2}$(∠A+∠C),即可求∠B的大小;
(2)在(1)的条件下,证明∠FED=∠FEG,即可证明CE平分∠DEG.
解答 (1)解:∵F为△ABC的内心,
∴∠AFE=$\frac{1}{2}$(∠A+∠C),
∵B、D、F、E四点共圆,
∴∠AFE=∠B=$\frac{1}{2}$(∠A+∠C),
∵∠A+∠B+∠C=180°,
∴∠B=60°;
(2)解:连接BF,
∵F为△ABC的内心,
∴∠EBF=∠DBF,
∵B、D、F、E四点共圆,
∴$\widehat{EF}$=$\widehat{DF}$,
∴EF=DF,
∴∠FED=∠FDE,
∵AD⊥EG,
∴∠GEF=30°,
∴∠FED=∠FEG=30°,
∴CE平分∠DEG.
点评 本题考查四点共圆的性质,考查三角形内心的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.不等式x>x2的解集是( )
| A. | {x|x<0} | B. | {x|x>0} | C. | {x|x<1} | D. | {x|0<x<1} |
3.若|x|≤1时都有|ax+b|≤1,则不等必成立的是( )
| A. | |a|≤|b|≤1 | B. | |b|≤|a|≤1 | C. | |a|≤1,|b|≤1 | D. | |a|+|b|≤1 |
10.已知f(x)=2x,则f-1(4)=( )
| A. | 1 | B. | 3 | C. | 2 | D. | -2 |