题目内容
5.已知cos(θ+$\frac{π}{4}$)=-$\frac{\sqrt{10}}{10}$,θ∈(0,$\frac{π}{2}$),则cos2θ=-$\frac{3}{5}$.分析 由条件利用同角三角函数的基本关系求得sin(θ+$\frac{π}{4}$)的值,再利用诱导公式、二倍角的正弦公式求得cos2θ=sin(2θ+$\frac{π}{2}$)的值.
解答 解:∵cos(θ+$\frac{π}{4}$)=-$\frac{\sqrt{10}}{10}$,θ∈(0,$\frac{π}{2}$),∴sin(θ+$\frac{π}{4}$)=$\sqrt{{1-cos}^{2}(θ+\frac{π}{4})}$=$\frac{3\sqrt{10}}{10}$,
则cos2θ=sin(2θ+$\frac{π}{2}$)=2sin(θ+$\frac{π}{4}$)cos(θ+$\frac{π}{4}$)=2×$\frac{3\sqrt{10}}{10}$×(-$\frac{\sqrt{10}}{10}$)=-$\frac{3}{5}$,
故答案为:-$\frac{3}{5}$.
点评 本题主要考查同角三角函数的基本关系,诱导公式,二倍角的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
16.已知角a的终边射线与单位圆交于点P($\frac{3}{5}$,$\frac{4}{5}$),那么tan2a的值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{24}{7}$ | D. | $\frac{24}{7}$ |
20.若a、b、c∈R,a>b,则下列不等式一定成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | $\frac{a}{b}$>1 | D. | a(c2+1)>b(c2+1) |
10.若cosα=$\frac{4}{5}$,则cos2α=( )
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
17.不等式|4x-1|>4的解集是( )
| A. | $\{x|x<-\frac{3}{4}$或$x>\frac{5}{4}\}$ | B. | $\{x|-\frac{3}{4}<x<\frac{5}{4}\}$ | C. | $\{x|x<-\frac{3}{4}\}$ | D. | $\{x|x>\frac{5}{4}\}$ |
14.已知角α的终边经过点P(-4m,-3),且$cosα=-\frac{4}{5}$,则m的值为( )
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
15.设全集U={a,b,c,d,e},集合M={a,c,d},N={b,d,e},那么(CUM)∩N是( )
| A. | ∅ | B. | {d} | C. | {a,c} | D. | {b,e} |
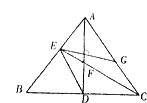 如图所示,在△ABC中,AD∩CE=F,AD⊥EG,且F为△ABC的内心.
如图所示,在△ABC中,AD∩CE=F,AD⊥EG,且F为△ABC的内心.