题目内容
5.$\frac{1}{2}$+$\frac{1}{2}$+$\frac{3}{8}$+…+$\frac{n}{{2}^{n}}$等于( )| A. | $\frac{{2}^{n}-n-1}{{2}^{n}}$ | B. | $\frac{{2}^{n+1}-n-2}{{2}^{n}}$ | C. | $\frac{{2}^{n}-n+1}{{2}^{n}}$ | D. | $\frac{{2}^{n+1}-n+2}{{2}^{n}}$ |
分析 通过记该数列通项公式an=$\frac{n}{{2}^{n}}$,利用Sn=1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n}}$与$\frac{1}{2}$Sn=1•$\frac{1}{{2}^{2}}$+2•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n}}$+n•$\frac{1}{{2}^{n+1}}$错位相减、计算即得结论.
解答 解:依题意,记该数列通项公式an=$\frac{n}{{2}^{n}}$,
∴数列的和Sn=1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n}}$,
∴$\frac{1}{2}$Sn=1•$\frac{1}{{2}^{2}}$+2•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n}}$+n•$\frac{1}{{2}^{n+1}}$,
两式相减得:$\frac{1}{2}$Sn=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-n•$\frac{1}{{2}^{n+1}}$,
∴Sn=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$
=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n}}$
=$\frac{-2-n+{2}^{n+1}}{{2}^{n}}$,
故选:B.
点评 本题考查数列的前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案| A. | x4-16(x≤-2或x≥2) | B. | x4-16(-2≤x≤2) | C. | x2-16(x≤-2或x≥2) | D. | x2-16(-2≤x≤2) |
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{7}$ |
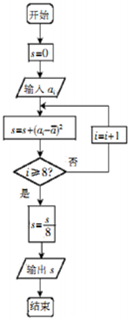 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| 39 | 40 | 42 | 42 | 43 | 45 | 46 | 47 |
| A. | A | B. | B | C. | C | D. | D |