题目内容
20.求和:S=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$+…+$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$.分析 通过通分、裂项计算可知$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$,进而并项相加即得结论.
解答 解:∵$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=$\sqrt{\frac{{n}^{2}(n+1)^{2}+(n+1)^{2}+{n}^{2}}{{n}^{2}(n+1)^{2}}}$
=$\sqrt{\frac{{n}^{4}+2{n}^{3}+3{n}^{2}+2n+1}{[{n(n+1)]}^{2}}}$
=$\sqrt{\frac{({{n}^{2}+n+1)}^{2}}{[{n(n+1)]}^{2}}}$
=$\frac{{n}^{2}+n+1}{n(n+1)}$
=1+$\frac{1}{n}$-$\frac{1}{n+1}$,
∴S=(1+1-$\frac{1}{2}$)+(1+$\frac{1}{2}$-$\frac{1}{3}$)+…+(1+$\frac{1}{n}$-$\frac{1}{n+1}$)
=n+1-$\frac{1}{n+1}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,裂项、并项相加是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
5.$\frac{1}{2}$+$\frac{1}{2}$+$\frac{3}{8}$+…+$\frac{n}{{2}^{n}}$等于( )
| A. | $\frac{{2}^{n}-n-1}{{2}^{n}}$ | B. | $\frac{{2}^{n+1}-n-2}{{2}^{n}}$ | C. | $\frac{{2}^{n}-n+1}{{2}^{n}}$ | D. | $\frac{{2}^{n+1}-n+2}{{2}^{n}}$ |
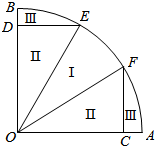 现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、
现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、