题目内容
(12分)已知二次函数f (x)= ,设方程f (x)
,设方程f (x)
=x的两个实根为x1和x2.
(1)如果x1<2<x2<4,且函数f (x)的对称轴为x=x0,求证:x0>—1;
(2)如果∣x1∣<2,,∣x2—x1∣=2,求 的取值范围.
的取值范围.
解:(1)设g(x)=" f" (x)—x
= ,且g(4)>0,即
,且g(4)>0,即
∴
(2)由g(x)= .
.
①若0<x1<2,则x2一x1=2,即x2=x1+2>2,∴g(2)=4a+2b—1<0,
又 ,代入上式得
,代入上式得
②若一2<x1<0,则x2=一2+x1<一2,∴g(一2)<0,即4a-2b+3<0,同理可求得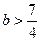 .
.
故当0<x1<2时,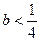 ;当一2<x1<0时,
;当一2<x1<0时,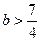 .
.
解析

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 ,其中
,其中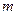 为常数
为常数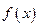 在R上是减函数.
在R上是减函数.
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有
 .
. ;
; 对所有
对所有 恒成立,求实数
恒成立,求实数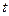 的取值范围.
的取值范围. 上的函数
上的函数 的图象如右图所示
的图象如右图所示
 的图像与
的图像与 轴的交点至少有一个在原点的右侧,求实数
轴的交点至少有一个在原点的右侧,求实数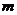 的取值范围。
的取值范围。 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为
的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为 .
.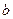 的取值范围;
的取值范围; ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
. 的解析式和值域;
的解析式和值域; ,使得当
,使得当 时,数列
时,数列 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,
恒成立,若存在,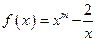 ,且
,且 。
。 的值;
的值; 的奇偶性;
的奇偶性; 上的单调性,并给予证明。
上的单调性,并给予证明。