题目内容
在平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为
的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为 .
.
(I)求实数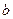 的取值范围;
的取值范围;
(II)求圆 的一般方程;
的一般方程;
(III)圆 是否经过某个定点(其坐标与
是否经过某个定点(其坐标与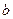 无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
解:(I)令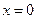 得抛物线与
得抛物线与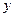 轴交点是
轴交点是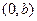 ;令
;令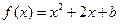 ,由题意
,由题意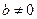 ,
,
且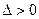 ,解得
,解得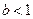 ,且
,且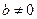 .
.
(II)设所求圆的一般方程为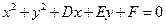 ,
,
令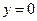 得,
得,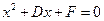 ,这与
,这与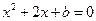 是同一个方程,故
是同一个方程,故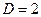 ,
,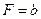 .
.
令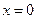 得,
得,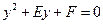 ,此方程有一个根为
,此方程有一个根为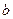 ,代入得出
,代入得出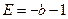 ,
,
所以圆 的一般方程为
的一般方程为 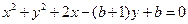 .
.
(III)圆 过定点
过定点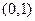 和
和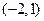 .
.
证明如下:
法1,直接将点的坐标代入验证;
法2,圆 的方程改写为
的方程改写为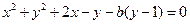 ,于是有
,于是有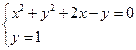 ,解得
,解得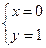 或
或 ,故过定点
,故过定点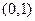 和
和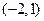 .
.
解析

练习册系列答案
相关题目
 是奇
是奇 有最小值2,且f (1)
有最小值2,且f (1) .
. ,设方程f (x)
,设方程f (x) 的取值范围.
的取值范围. 且
且 。
。 的解析式及定义域。(Ⅱ)求
的解析式及定义域。(Ⅱ)求 且
且 。
。 的解析式及定义域。
的解析式及定义域。 ,函数
,函数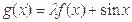 是区间
是区间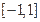 上的减函数.
上的减函数. 的最大值;
的最大值;  上恒成立,求
上恒成立,求 的取值范围.
的取值范围. 的定义域为
的定义域为 。
。 的值域;
的值域; 。(1)求不等式
。(1)求不等式 的解
的解 的解集为R,求实数m的取值范围。
的解集为R,求实数m的取值范围。