Question

【题目】设m∈R，函数f（x）=ex﹣m（x+1） m2（其中e为自然对数的底数）
（Ⅰ）若m=2，求函数f（x）的单调递增区间；
（Ⅱ）已知实数x1 ， x2满足x1+x2=1，对任意的m＜0，不等式f（x1）+f（0）＞f（x2）+f（1）恒成立，求x1的取值范围；
（Ⅲ）若函数f（x）有一个极小值点为x0 ， 求证f（x0）＞﹣3，（参考数据ln6≈1.79）

Answer 1

【答案】解：（Ⅰ）m=2时，f（x）=ex﹣2x﹣1，f′（x）=ex﹣2，

令f′（x）＞0，解得：x＞ln2，

故函数f（x）在[ln2，+∞）递增；

（Ⅱ）∵不等式f（x1）+f（0）＞f（x2）+f（1）恒成立，x1+x2=1，

∴2（x1﹣1）m﹣（ ﹣ ）+e﹣1＜0对任意m＜0恒成立，

令g（m）=2（x1﹣1）m﹣（ ﹣ ）+e﹣1，

当2（x1﹣1）=0时，g（m）=0＜0不成立，

则 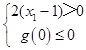，解得：x1＞1；

（Ⅲ）由题意得f′（x）=ex﹣m，f′（x0）=0，故 =m，

f（x0）= ﹣m（x0+1）+ m2= m2﹣mlnm，m＞0，

记h（m）= m2﹣mlnm，m＞0，

h′（m）= m﹣lnm﹣1，h′′（m）= ﹣ ，

当0＜m＜2时，h′′（m）＜0，当m＞2时，h′′（m）＞0，

故函数h′（x）在（0，2）递减，在（2，+∞）递增，

如图所示：

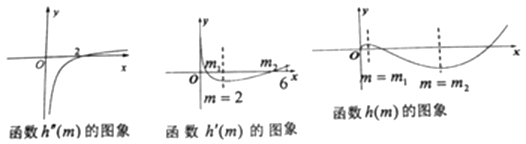
[h′（m）]min=h′（2）=﹣ln2＜0，

又当m→0时，h′（m）＞0，m→+∞，h′（m）＞0，

故函数h′（m）=0有2个根，记为m1，m2（m1＜2＜m2＜6），（h′（6）＞0），

故h（m）在（0，m1）递增，在（m1，m2）递减，在（m2，+∞）递增，

又当m→0时，h（m）＞0，h（m）在m2处取极小值，

由h′（m2）=0， m2﹣lnm2﹣1=0，lnm2= m2﹣1，

故h（m2）= ﹣m2lnm2= ﹣m2（ m2﹣1）

=﹣ +m2=﹣ +1∈（﹣3，1），

故f（x0）＞﹣3

【解析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的递增区间即可；（Ⅱ）问题转化为2（x1﹣1）m﹣（ ﹣ ）+e﹣1＜0对任意m＜0恒成立，令g（m）=2（x1﹣1）m﹣（ ﹣ ）+e﹣1，得到关于x1的不等式组，解出即可；（Ⅲ）求出f（x0）的解析式，记h（m）= m2﹣mlnm，m＞0，根据函数的单调性求出h（m）的取值范围，从而求出f（x0）的范围，证明结论即可．
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．