题目内容
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
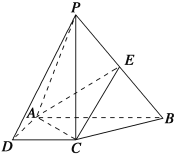
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】(1)∵PC⊥平面ABCD,AC平面ABCD,∴AC⊥PC.∵AB=2,AD=CD=1,∴AC=BC=![]() .
.
∴AC2+BC2=AB2.∴AC⊥BC.
又BC∩PC=C,∴AC⊥平面PBC.
∵AC平面EAC,
∴平面EAC⊥平面PBC.
(2)如图,以点C为原点,![]() ,
,![]() ,
,![]() 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,
分别为x轴、y轴、z轴正方向,建立空间直角坐标系,
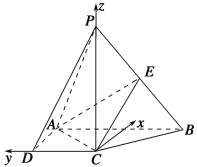
则C(0,0,0),A(1,1,0),B(1,-1,0),设P(0,0,a)(a>0),
则E![]() ,
,![]() =(1,1,0),
=(1,1,0),![]() =(0,0,a),
=(0,0,a),![]() =
=![]() .取m=(1,-1,0),则m·
.取m=(1,-1,0),则m·![]() =m·
=m·![]() =0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·
=0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·![]() =n·
=n·![]() =0,即
=0,即![]() 取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cos〈m,n〉|=
取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cos〈m,n〉|=![]() =
=![]() =
=![]() ,则a=2.于是n=(2,-2,-2),
,则a=2.于是n=(2,-2,-2),![]() =(1,1,-2).设直线PA与平面EAC所成角为θ,则sin θ=|cos〈
=(1,1,-2).设直线PA与平面EAC所成角为θ,则sin θ=|cos〈![]() ,n〉|=
,n〉|=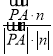 =
=![]() ,即直线PA与平面EAC所成角的正弦值为
,即直线PA与平面EAC所成角的正弦值为![]()

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案【题目】随机调查某社区80个人,以研究这一社区居民的休闲方式是否与性别有关,得到下面的数据表:
休闲方式 | 看电视 | 运动 | 合计 |
男性 | 20 | 10 | 30 |
女性 | 45 | 5 | 50 |
合计 | 65 | 15 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人是以运动为休闲方式的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,能否有99%的把握认为休闲方式与性别有关系?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ),其中n=a+b+c+d)
),其中n=a+b+c+d)