题目内容
已知函数f(x)=
.
(1)求f(x)的单调区间;
(2)求曲线y=f(x)在点x=1处的切线方程;
(3)求曲线y=f(x),y=|x|所围成的图形的面积S.
| 3 | x2 |
(1)求f(x)的单调区间;
(2)求曲线y=f(x)在点x=1处的切线方程;
(3)求曲线y=f(x),y=|x|所围成的图形的面积S.
(1)∵f(x)=
=x
,∴f′(x)=
x-
解f'(x)>0得x>0,解f'(x)<0得x<0,
∴f(x)的单调增区间是(0,+∞),单调减区间是(-∞,0)
(注:也可以写成闭区间[0,+∞)或(-∞,0])…(4分)
(2)切点坐标是(1,1),且f′(1)=
,
∴y=f(x)在点x=1处的切线方程是y-1=
(x-1)
化简得2x-3y+1=0…(9分)
(3)解
=|x|得x=±1,0
由f(x)=
的图象特点得曲线y=f(x),y=|x|所围成的图形的面积是:
S=2
(x
-x)dx=2(
x
-
)
=
.(14分)
| 3 | x2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
解f'(x)>0得x>0,解f'(x)<0得x<0,
∴f(x)的单调增区间是(0,+∞),单调减区间是(-∞,0)
(注:也可以写成闭区间[0,+∞)或(-∞,0])…(4分)
(2)切点坐标是(1,1),且f′(1)=
| 2 |
| 3 |
∴y=f(x)在点x=1处的切线方程是y-1=
| 2 |
| 3 |
化简得2x-3y+1=0…(9分)
(3)解
| 3 | x2 |
由f(x)=
| 3 | x2 |
S=2
| ∫ | 10 |
| 2 |
| 3 |
| 3 |
| 5 |
| 5 |
| 3 |
| x2 |
| 2 |
| | | 10 |
| 1 |
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
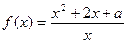
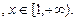 当
当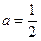 时,求函数
时,求函数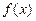 的最小值;
的最小值; 取极小值时,
取极小值时, 的值是( )
的值是( )



 的极大值是( )
的极大值是( )



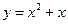 ,则在闭区间
,则在闭区间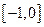 上的最小值是( )
上的最小值是( )