题目内容
已知函数f(x)=ax+lnx(a∈R),
(Ⅰ)若a=-1,求曲线y=f(x)在x=
处的切线的斜率;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=2x-2,若存在x1∈(0,+∞),对于任意x2∈[0,1],使f(x1)≥g(x2),求a的范围.
(Ⅰ)若a=-1,求曲线y=f(x)在x=
| 1 |
| 2 |
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设g(x)=2x-2,若存在x1∈(0,+∞),对于任意x2∈[0,1],使f(x1)≥g(x2),求a的范围.
(Ⅰ)∵f(x)=ax+lnx,∴f′(x)=
(x>0)
若a=-1,k=f′(
)=-1+2=1
(Ⅱ)当a≥0,f′(x)>0,∴f(x)在(0,+∞)为增函数
当a<0,令f′(x)>0,∴0<x<-
,f′(x)<0,∴x>-
,
综上:a≥0,f(x)的单调增区间为(0,+∞);a<0时,f(x)的单调增区间为(0,-
),单调减区间为(-
,+∞);
(Ⅲ)由(Ⅱ)知,当a≥0时,符合题意;
当a<0时,f(x)的单调增区间为(0,-
),单调减区间为(-
,+∞)
∴f(x)max=f(-
)=-1+ln(-
)
由题意知,只需满足f(x)max≥g(x)max=g(1)=0,∴-1+ln(-
)≥0,
∴-
≤a<0
综上:a≥-
| ax+1 |
| x |
若a=-1,k=f′(
| 1 |
| 2 |
(Ⅱ)当a≥0,f′(x)>0,∴f(x)在(0,+∞)为增函数
当a<0,令f′(x)>0,∴0<x<-
| 1 |
| a |
| 1 |
| a |
综上:a≥0,f(x)的单调增区间为(0,+∞);a<0时,f(x)的单调增区间为(0,-
| 1 |
| a |
| 1 |
| a |
(Ⅲ)由(Ⅱ)知,当a≥0时,符合题意;
当a<0时,f(x)的单调增区间为(0,-
| 1 |
| a |
| 1 |
| a |
∴f(x)max=f(-
| 1 |
| a |
| 1 |
| a |
由题意知,只需满足f(x)max≥g(x)max=g(1)=0,∴-1+ln(-
| 1 |
| a |
∴-
| 1 |
| e |
综上:a≥-
| 1 |
| e |

练习册系列答案
相关题目
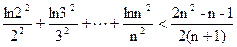 (n∈N
(n∈N ,n≥2)
,n≥2) 的极大值是( )
的极大值是( )


