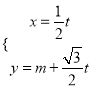题目内容
【题目】已知正项数列{an},a1=1,an=an+12+2an+1(Ⅰ)求证:数列{log2(an+1)}为等比数列:
(Ⅱ)设bn=n1og2(an+1),数列{bn}的前n项和为Sn , 求证:1≤Sn<4.
【答案】解:(Ⅰ)∵an=an+12+2an+1 , ∴an+1=(an+1+1)2 ,
∵an>0,
∴2log2(an+1+1)=log2(an+1),
即log2(an+1+1)= ![]() log2(an+1),
log2(an+1),
即数列{log2(an+1)}是1为首项, ![]() 为公比的等比数列:
为公比的等比数列:
(Ⅱ)∵数列{log2(an+1)}是1为首项, ![]() 为公比的等比数列:
为公比的等比数列:
∴log2(an+1)= ![]() ,
,
设bn=n1og2(an+1)=n ![]() ,
,
则数列{bn}的前n项和为Sn=1+ ![]() ,
,![]() Sn=
Sn= ![]() .
.
两式相减得 ![]() Sn=1+
Sn=1+ ![]() =2[1﹣(
=2[1﹣( ![]() )n]﹣
)n]﹣ ![]() ,
,
∴Sn=4﹣ ![]() .
.
∵bn=n ![]() >0,
>0,
∴Sn≥S1=1,
∴1≤Sn<4
【解析】(Ⅰ)根据数列的递推关系结合等比数列的定义即可证明数列{log2(an+1)}为等比数列:(Ⅱ)求出bn=n1og2(an+1)的表达式,利用错位相减法即可求出数列{bn}的前n项和为Sn .
【考点精析】本题主要考查了等比关系的确定和数列的前n项和的相关知识点,需要掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系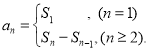 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目