题目内容
15．若向量 $\overrightarrow{a}$=（2，m），$\overrightarrow{b}$=（1，-3）满足$\overrightarrow{a}$⊥$\overrightarrow{b}$，则实数m的值为$\frac{2}{3}$．分析 根据向量垂直的等价条件进行求解即可．
解答 解：∵向量 $\overrightarrow{a}$=（2，m），$\overrightarrow{b}$=（1，-3）满足$\overrightarrow{a}$⊥$\overrightarrow{b}$，
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2-3m=0，
解得m=$\frac{2}{3}$，
故答案为：$\frac{2}{3}$
点评 本题主要考查向量数量积的应用，根据向量垂直的坐标公式进行求解是解决本题的关键．
练习册系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
6．已知A，B，C为△ABC的三个内角，命题p：A=B；命题q：sinA=sinB．则￢p是￢q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
3．已知等差数列{an}满足：a3=13，a13=33，则数列{an}的公差为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
10．若函数f（x）=$\sqrt{3}$cos（2x+α）-sin（2x+α）的图象关于直线x=0对称，则α=（ ）
| A． | α=kπ-$\frac{π}{3}$ （k∈Z） | B． | α=kπ-$\frac{π}{6}$ （k∈Z） | C． | α=kπ+$\frac{π}{3}$（k∈Z） | D． | α=kπ+$\frac{π}{6}$ （k∈Z） |
20．如图是一个几何体的三视图，其俯视图的面积为8$\sqrt{2}$，则该几何体的表面积为（ ）
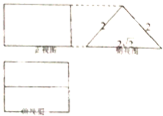
| A． | 8 | B． | 20+8$\sqrt{2}$ | C． | 16 | D． | 24+8$\sqrt{2}$ |
4．若$\frac{cos（2α-π）}{sin（α+\frac{π}{4}）}$=$\frac{\sqrt{2}}{2}$，则sinα-cosα的值为（ ）
| A． | -$\frac{\sqrt{7}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{7}}{2}$ |
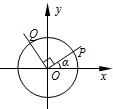在平面直角坐标系xOy中，设锐角α的始边与x轴的非负半轴重合，终边与单位圆交于点P（x1，y1），将射线OP绕坐标原点O按逆时针方向旋转$\frac{π}{2}$后与单位圆交于点Q（x2，y2）．记f（α）=y1+y2．