题目内容
设函数y=f(x)是定义在R上的函数,当x<0时,f(x)>1,对任意实数x、y∈R,有f(x+y)=f(x)·f(y).(1)求证:f(0)=1,且当x>0时,有0<f(x)<1;
(2)若数列{an}满足a1=f(0),且f(an+1)=![]() ,n∈N*.
,n∈N*.
①求an;
②若不等式(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )≥k
)≥k![]() ,对于n∈N*都成立,求k的最大值.
,对于n∈N*都成立,求k的最大值.
(1)证明:令x=0,y=-1,则f(-1)=f(0)·f(-1).∵f(-1)>1,
∴f(0)=1,
又当x>0时,-x<0,f(-x)>1,
而f(x)·f(-x)=f(0)=1,∴f(-x)=![]() >1.
>1.
∴0<f(x)<1.
(2)①a1=f(0)=1,f(an+1)·f(-an-2)=1,∴f(an+1-an-2)=1.
由已知条件及第(1)小题的结论知,只能有:
an+1-an-2=0,∴an+1-an=2,
an=2n-1.
②∵![]() >0,∴原问题可转化为:
>0,∴原问题可转化为:
k≤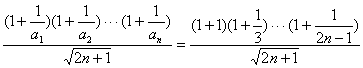 ,对n∈N*都成立.
,对n∈N*都成立.
令Cn=(1+1)(1+![]() )…(1+
)…(1+![]() ),容易证明Cn+1>Cn
),容易证明Cn+1>Cn
即{Cn}为递增数列,因此K≤C1=![]() .
.
∴kmax=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )=1,
)=1, ,
,