题目内容
设函数y=f(x)是定义在R上的奇函数，当x＞0,f(x)=x2-2x+3,试求出f(x)在R上的表达式，并画出它的图象，根据图象写出单调区间.
解析：∵f(x)是R上的奇函数，∴f(0)=0.
当x＜0时，则-x＞0,
∴f(x)=-f(-x)=-(x2+2x+3),
∴f(x)=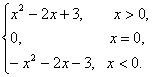
其图象如下图所示.
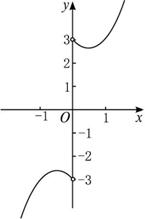
由图象得单调增区间是（-∞,-1]，［1,+∞），
单调减区间是［-1,0］,(0,1].
练习册系列答案
相关题目
题目内容
设函数y=f(x)是定义在R上的奇函数，当x＞0,f(x)=x2-2x+3,试求出f(x)在R上的表达式，并画出它的图象，根据图象写出单调区间.
解析：∵f(x)是R上的奇函数，∴f(0)=0.
当x＜0时，则-x＞0,
∴f(x)=-f(-x)=-(x2+2x+3),
∴f(x)=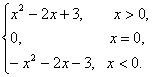
其图象如下图所示.
由图象得单调增区间是（-∞,-1]，［1,+∞），
单调减区间是［-1,0］,(0,1].
)=1，
，