题目内容
16.若直线kx-y+2k=0与椭圆$\frac{{x}^{2}}{4}$+y2=1相交于A、B两点,P(2,0),则使△APB面积取得最大值时k=$±\frac{1}{2}$.分析 求出直线经过的定点,画出图形判断三角形APB面积取得最大值时的情况,然后求出k即可.
解答 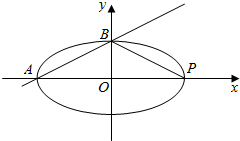 解:直线kx-y+2k=0经过定点(-2,0)是椭圆$\frac{{x}^{2}}{4}$+y2=1的左顶点,即A、B两点之一,
解:直线kx-y+2k=0经过定点(-2,0)是椭圆$\frac{{x}^{2}}{4}$+y2=1的左顶点,即A、B两点之一,
P(2,0),是椭圆的右顶点,如图:
使△APB面积取得最大值时,B是椭圆的上顶点或下顶点,
可得k=$±\frac{1}{2}$.
故答案为:$±\frac{1}{2}$.
点评 本题考查直线与椭圆的位置关系的应用,考查计算能力.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2.
如图所示,在四较锥E-ABCD中,底面ABCD为矩形,CD⊥平面BEC,G是线段BE上一点,F是线段DC的中点且GF∥平面ADE,AB=BE=EC=2. 如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.
如图所示,⊙O的直径的长是关于x的二次方程x2+2(k-2)x+k=0(k是整数)的最大整数根.P是⊙O外一点,过点P作⊙O的切线PA和割线PBC,其中A为切点,点B,C是直线PBC与⊙O的交点.若PA,PB,PC的长都是正整数,且PB的长不是合数,求PA2+PB2+PC2的值.