题目内容
4.已知f(x)=x2-2x-3,等差数列{an}中,a1=f(x-1),a${\;}_{2}=-\frac{3}{2}$,a3=f(x)求:(1)x的值;
(2)通项an.
分析 (1)首先根据所给的函数式f(x)=x2-2x-3,写出数列的第二项和第三项,利用等差中项公式求解即可.
(2)根据等差数列特点求出x的值,求出公差,即可写出通项公式.
解答 解:(1)∵f(x)=x2-2x-3,
∴a1=f(x-1)=(x-2)2-4,
a3=(x-1)2-4.
又a1+a3=2a2,a${\;}_{2}=-\frac{3}{2}$,解得x=0,或x=3.
(2)由(1)知a1,a2,a3分别是0,-$\frac{3}{2}$,-3或-3,-$\frac{3}{2}$,0.
当a1=0,a2=-$\frac{3}{2}$,a3=-3时,d=a2-a1=-$\frac{3}{2}$,
an=a1+(n-1)d=-$\frac{3}{2}$(n-1);
当a1=-3,a2=-$\frac{3}{2}$,a3=0时,d=a2-a1=$\frac{3}{2}$,
an=a1+(n-1)d=-3+$\frac{3}{2}$(n-1)=$\frac{3}{2}$(n-3).
∴an=-$\frac{3}{2}$(n-1)或an=$\frac{3}{2}$(n-3).
点评 本题考查等差数列的性质和应用,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
12.直线l交椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1与M,N两点,椭圆的上顶点为B点,若△BMN的重心坐标为($\frac{1}{3}$,$\frac{1}{3}$),则直线l的方程是( )
| A. | 2x-4y+3=0 | B. | 2x-4y-3=0 | C. | 4x-2y-3=0 | D. | x-y-5=0 |
 装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算:
装潢师小王在墙面上设计了如图所示的一个图案,已知四边形四个顶点都在圆周上,且AD=DC=4m,BC=6m,∠A=120°,现在小王想买乳胶漆给四边形ABCD涂色,依据设计方案四边形的四边涂成红色,四边形内部要涂成蓝色,他想根据线段的长度与四边形的面积来买乳胶漆.请你帮他计算: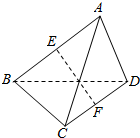 如图:在三棱锥A-BCD中,E,F分别是AB,CD的中点,且EF=5,AC=6,BD=8,则异面直线AC与BD的夹角为多少?
如图:在三棱锥A-BCD中,E,F分别是AB,CD的中点,且EF=5,AC=6,BD=8,则异面直线AC与BD的夹角为多少?