题目内容
10．圆（x-1）2+（y-2）2=1关于直线y=x对称的圆的方程为（x-2）2+（y-1）2=1．分析 求出圆心（1，2）关于直线y=x对称的点的坐标，可得要求的对称圆的方程．
解答 解：由于圆心（1，2）关于直线y=x对称的点的坐标为（2，1），半径为1，
故圆（x-1）2+（y-2）2=1关于直线y=x对称的圆的方程为 （x-2）2+（y-1）2=1，
故答案为：（x-2）2+（y-1）2=1．
点评 本题主要考查求一个圆关于一条直线的对称的圆的方程的方法，关键是求出对称圆的圆心坐标，属于基础题．
练习册系列答案
考前必练系列答案
相关题目
18．已知某简谐运动的图象经过点（0，2），且对应函数的解析式为f（x）=4sin（$\frac{π}{3}$x+φ）（|φ|＜$\frac{π}{2}$），则该简谐运动的初相φ的值为（ ）
| A． | φ=$\frac{π}{3}$ | B． | φ=$\frac{π}{4}$ | C． | φ=$\frac{π}{5}$ | D． | φ=$\frac{π}{6}$ |
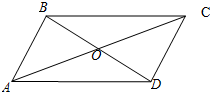如图，在平行四边形ABCD中，BD，AC相交于点O，设向量$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow b$．
2．假设四边形ABCD为圆内接正方形，向圆内随机地投一点，则点落在正方形ABCD内的概率为（ ）
| A． | $\frac{\sqrt{2}}{2π}$ | B． | $\frac{1}{π}$ | C． | $\frac{\sqrt{2}}{π}$ | D． | $\frac{2}{π}$ |
