题目内容
16.设函数f(x)的定义域为D,若存在闭区间[m,n]⊆D,使得函数f(x)满足:①f(x)在[m,n]上是单调函数;②f(2)在[m,n]上的值域为[2m,2n],则称区间[m,n]为y=f(x)的“倍值区间”,函数f(x)称为倍值函数.如函数f(x)=2x的倍值区间是[1,2].(1)判断函数f(x)=3x是否是倍值区间(无须说明理由);
(2)求函数f(x)=x2(x≥0)的倍值区间;
(3)证明函数h(x)=loga($\frac{3}{4}$ax-$\frac{1}{8}$)是倍值函数,并求出倍值区间.
分析 根据已知可得若函数f(x)存在“倍值区间”,则函数f(x)=2x,在定义域至少存在两个不相等的根,逐一判断,可得结论.
解答 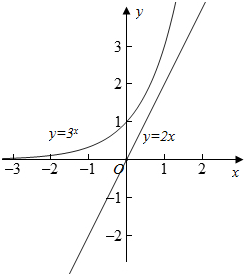 解:函数中存在“倍值区间”,则:①f(x)在[m,n]内是单调函数;②$\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.$,或$\left\{\begin{array}{l}{f(m)=2n}\\{f(n)=2m}\end{array}\right.$.
解:函数中存在“倍值区间”,则:①f(x)在[m,n]内是单调函数;②$\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.$,或$\left\{\begin{array}{l}{f(m)=2n}\\{f(n)=2m}\end{array}\right.$.
(1),若存在“倍值区间”[m,n],
则$\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.$,∴$\left\{\begin{array}{l}{{3}^{a}=2a}\\{{3}^{b}=2b}\end{array}\right.$,
则m,n是方程3x-2x=0的两根,
分别画出y=3x与y=2x的图象,
由图象可知3x-2x=0无根,
故函数不存在“倍值区间”;
(2)f(x)=x2(x≥0),若存在“倍值区间”[m,n],
则$\left\{\begin{array}{l}{f(m)=2m}\\{f(n)=2n}\end{array}\right.$,∴$\left\{\begin{array}{l}{{m}^{2}=2m}\\{{n}^{2}=2n}\end{array}\right.$,
则m,n是方程x2-2x=0的两根,
∴$\left\{\begin{array}{l}{m=0}\\{n=2}\end{array}\right.$,
∴f(x)=x2(x≥0),存在“倍值区间”[0,2];
(3)h(x)=loga($\frac{3}{4}$ax-$\frac{1}{8}$).不妨设a>1,则函数在定义域内为单调增函数
若存在“倍值区间”[m,n],
则$\left\{\begin{array}{l}{h(m)=2m}\\{h(n)=2n}\end{array}\right.$,
∴$\left\{\begin{array}{l}{lo{g}_{a}(\frac{3}{4}{a}^{m}-\frac{1}{8})=2m}\\{lo{g}_{a}(\frac{3}{4}{a}^{n}-\frac{1}{8})=2n}\end{array}\right.$,
∴m,n是方程loga($\frac{3}{4}$ax-$\frac{1}{8}$)=2x的两个根,
∴m,n是方程a2x-$\frac{3}{4}$ax+$\frac{1}{8}$=0的两个根,
设ax=t,t>0,
∴t2-$\frac{3}{4}$t+$\frac{1}{8}$=0,
解得m=$\frac{1}{4}$,n=$\frac{1}{2}$,
故存在“倍值区间”[$\frac{1}{4}$,$\frac{1}{2}$];
点评 本题考查的知识点是函数图象和性质,其中正确理解函数f(x)存在“倍值区间”的含义,是解答的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 204种 | B. | 96种 | C. | 240种 | D. | 384种 |
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |