题目内容
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]()
![]() 的上顶点坐标为
的上顶点坐标为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)若椭圆上的点![]() 的横坐标为
的横坐标为![]() ,且位于第一象限,点
,且位于第一象限,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,
,![]() 是位于直线
是位于直线![]() 异侧的椭圆上的动点.
异侧的椭圆上的动点.
①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②若动点![]() 满足
满足![]() ,试探求直线
,试探求直线![]() 的斜率是否为定值?说明理由.
的斜率是否为定值?说明理由.
【答案】(1)![]() (2)①
(2)①![]() ②为定值,见解析
②为定值,见解析
【解析】
(1)直接根据椭圆的几何性质求解;
(2)由(1)可得![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,
①设直线![]() 方程,联立椭圆方程,设
方程,联立椭圆方程,设![]() ,得韦达定理,表示出四边形
,得韦达定理,表示出四边形![]() 面积
面积![]() ,从而求出四边形
,从而求出四边形![]() 面积最大值为
面积最大值为![]() ;
;
②由题意可得直线![]() 斜率与直线
斜率与直线![]() 斜率互为相反数,设直线
斜率互为相反数,设直线![]() 的方程,联立椭圆方程,设
的方程,联立椭圆方程,设![]() ,得两根之和,求得
,得两根之和,求得![]() ,设
,设![]() ,同理可得
,同理可得![]() ,根据斜率计算公式得直线
,根据斜率计算公式得直线![]() 的斜率为定值.
的斜率为定值.
解:(1)由题意![]() ,可得
,可得![]() ,
,
则椭圆的标准方程为![]() ;
;
(2)由(1)可得![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,
①设直线![]() 方程为
方程为![]() ,联立椭圆方程
,联立椭圆方程![]() ,
,
化简可得![]() ,
,
设![]() ,则
,则![]() ,
,
![]()
![]()
![]()
![]()
![]()
∴当![]() 时,四边形
时,四边形![]() 面积最大值为
面积最大值为![]() ;
;
②由题意,因为![]() ,则直线
,则直线![]() 斜率与直线
斜率与直线![]() 斜率互为相反数,
斜率互为相反数,
设直线![]() 的方程为
的方程为![]() ,联立椭圆方程
,联立椭圆方程![]() ,
,
化简可得![]() ,设
,设![]() ,
,
则![]() ,又
,又![]() ,所以
,所以![]() ,
,
设![]() ,同理可得
,同理可得![]() ,
,
所以![]() ,
,
所以直线![]() 的斜率
的斜率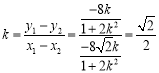 为定值.
为定值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某工厂生产![]() 、
、![]() 两种零件,其质量测试按指标划分,指标大于或等于
两种零件,其质量测试按指标划分,指标大于或等于![]() 的为正品,小于
的为正品,小于![]() 的为次品.现随机抽取这两种零件各100个进行检测,检测结果统计如下:
的为次品.现随机抽取这两种零件各100个进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
| 8 | 12 | 40 | 30 | 10 |
| 9 | 16 | 40 | 28 | 7 |
(Ⅰ)试分别估计![]() 、
、![]() 两种零件为正品的概率;
两种零件为正品的概率;
(Ⅱ)生产1个零件![]() ,若是正品则盈利50元,若是次品则亏损10元;生产1个零件
,若是正品则盈利50元,若是次品则亏损10元;生产1个零件![]() ,若是正品则盈利60元,若是次品则亏损15元,在(Ⅰ)的条件下:
,若是正品则盈利60元,若是次品则亏损15元,在(Ⅰ)的条件下:
(i)设![]() 为生产1个零件
为生产1个零件![]() 和一个零件
和一个零件![]() 所得的总利润,求
所得的总利润,求![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5个零件![]() 所得利润不少于160元的概率.
所得利润不少于160元的概率.