[题目]在直角坐标系中.曲线的参数方程为(为参数).若以该直角坐标系的原点为极点.轴的正半轴为极轴建立极坐标系.曲线的极坐标方程为:(其中为常数).(1)若曲线与曲线有两个不同的公共点.求的取值范围,(2)当时.求曲线上的点与曲线上点的最小距离. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在直角坐标系中，曲线的参数方程为（为参数），若以该直角坐标系的原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为：（其中为常数）.

（1）若曲线与曲线有两个不同的公共点，求的取值范围；

（2）当时，求曲线上的点与曲线上点的最小距离.

【答案】（Ⅰ）或;（Ⅱ）．

【解析】

试题消去参数把曲线的参数方程化为普通方程，利用公式把曲线的极坐标方

程化为直角坐标方程，利用数形结合的思想可以得出曲线有一个公共点时的的范围；（2）直线

N:，设M上点为，，则，由此可求

得最小值．

试题解析：对于曲线M,消去参数，得普通方程为,曲线是抛物线的一部分；对于曲线N，化成直角坐标方程为，曲线N是一条直线．（2分）

（1）若曲线M,N只有一个公共点，则有直线N过点时满足要求，并且向左下方平行运动直到过点之前总是保持只有一个公共点，再接着向左下方平行运动直到相切之前总是有两个公共点，所以满足要求；相切时仍然只有一个公共点，由，得，求得．综合可求得的取值范围是：或．（6分）

（2）当时，直线N:，设M上点为，，则

，

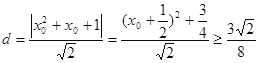当时取等号，满足，所以所求的最小距离为．（10分）

练习册系列答案

相关题目

【题目】在某区“创文明城区”（简称“创城”）活动中，教委对本区四所高中学校按各校人数分层抽样，随机抽查了100人，将调查情况进行整理后制成下表：

学校
抽查人数	50	15	10	25
“创城”活动中参与的人数	40	10	9	15

（注：参与率是指：一所学校“创城”活动中参与的人数与被抽查人数的比值）假设每名高中学生是否参与”创城”活动是相互独立的.

（1）若该区共2000名高中学生，估计学校参与“创城”活动的人数；

（2）在随机抽查的100名高中学生中，随机抽取1名学生，求恰好该生没有参与“创城”活动的概率；

（3）在上表中从两校没有参与“创城”活动的同学中随机抽取2人，求恰好两校各有1人没有参与“创城”活动的概率是多少？

【题目】“微信运动”是手机推出的多款健康运动软件中的一款，大学生M的微信好友中有400位好友参与了“微信运动”．他随机抽取了40位参与“微信运动”的微信好友（女20人，男20人）在某天的走路步数，经统计，其中女性好友走路的步数情况可分为五个类别：、步，（说明：“”表示大于或等于0，小于2000，以下同理），、步，、步，、步，、步，且、、三种类别的人数比例为，将统计结果绘制如图所示的柱形图；男性好友走路的步数数据绘制如图所示的频率分布直方图．

（Ⅰ）若以大学生抽取的微信好友在该天行走步数的频率分布，作为参与“微信运动”的所有微信好友每天走路步数的概率分布，试估计大学生的参与“微信运动”的400位微信好友中，每天走路步数在的人数；

（Ⅱ）若在大学生该天抽取的步数在的微信好友中，按男女比例分层抽取6人进行身体状况调查，然后再从这6位微信好友中随机抽取2人进行采访，求其中至少有一位女性微信好友被采访的概率．

【题目】若变量，满足约束条件，且最小值为7，则的值为（）

A. 1B. 2C. -2D. -1

【题目】在四棱锥中，底面为平行四边形，，，，点在底面内的射影在线段上，且，，M在线段上，且．

（Ⅰ）证明：平面；

（Ⅱ）在线段AD上确定一点F，使得平面平面PAB，并求三棱锥的体积．

【题目】在直角坐标系中，已知椭圆的上顶点坐标为，离心率为.

（1）求椭圆的标准方程；

（2）若椭圆上的点的横坐标为，且位于第一象限，点关于轴的对称点为点，是位于直线异侧的椭圆上的动点.

①若直线的斜率为，求四边形面积的最大值；

②若动点满足，试探求直线的斜率是否为定值？说明理由.

【题目】如果是抛物线上的点，它们的横坐标依次为，是抛物线的焦点，若，则_______________．

【题目】2019年初，某市为了实现教育资源公平，办人民满意的教育，准备在今年8月份的小升初录取中在某重点中学实行分数和摇号相结合的录取办法．该市教育管理部门为了了解市民对该招生办法的赞同情况，随机采访了440名市民，将他们的意见和是否近三年家里有小升初学生的情况进行了统计，得到如下的2×2列联表.

	赞同录取办法人数	不赞同录取办法人数	合计
近三年家里没有小升初学生	180	40	220
近三年家里有小升初学生	140	80	220
合计	320	120	440