题目内容

14．（x+$\frac{y}{x}$）6的展开式中，x-2y4的系数为15．

分析 先求得二项式展开式的通项公式，即可求得x-2y4的系数．

解答 解：（x+$\frac{y}{x}$）6的展开式的通项公式为Tr+1=${C}_{6}^{r}$•x6-2r•yr，
令r=4，可得x-2y4的系数为15，
故答案为：15．

点评 本题主要考查二项式定理，二项式展开式的通项公式的应用，属于基础题．

练习册系列答案
相关题目
4．两个向量相等的充要条件是它们的（　　）
A．长度相等B．长度相等，方向相同
C．方向相同D．面积相等
5．下列式子中正确的是（　　）
A．|$\overrightarrow{a}$|$\overrightarrow{a}$=$\overrightarrow{a}$2B．（$\overrightarrow{a}$•$\overrightarrow{b}$）2=$\overrightarrow{a}$2$\overrightarrow{b}$2C．$\overrightarrow{a}$（$\overrightarrow{a}$•$\overrightarrow{b}$）=$\overrightarrow{b}$•$\overrightarrow{a}$2D．|$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$|
2．已知圆C过点P（1，1），且与圆M：（x+2）2+（y+2）2=r2（r＞0）关于直线x+y+2=0对称．
（1）求圆C的方程；
（2）设Q为圆C上的一个点，$\overrightarrow{PQ}$•$\overrightarrow{MQ}$=-4，求点Q的坐标．
9．已知U={x|-3≤x＜5，x∈Z}，A={x|-2＜x＜4，x∈N}，B={-2，-1，0，1}，求：A∩B，∁UA，∁U（A∪B）．
19．已知一组数据为-1，0，3，5，x．它们的方差为6.8，则x的值为（　　）
A．-2或5.5B．2或-5.5C．4或11D．-4或-11
6．cos2（$\frac{x}{2}$-$\frac{7}{8}$π）-cos2（$\frac{x}{2}$+$\frac{7π}{8}$）可化简为（　　）
A．$\sqrt{2}$sinxB．-$\sqrt{2}$sinxC．$\frac{\sqrt{2}}{2}$sinxD．-$\frac{\sqrt{2}}{2}$sinx
4．设复数$\frac{1-i}{2+i}$=x+yi，其中x，y∈R，则x+y=（　　）
A．$-\frac{2}{3}$B．$\frac{2}{3}$C．$\frac{2}{5}$D．$-\frac{2}{5}$
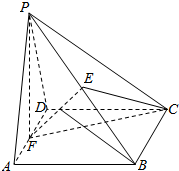5．如图，已知四棱锥P-ABCD的底面ABCD是边长为1的正方形，PD⊥底面ABCD，且PD=1，点E，F分别是棱PB，AD的中点．
（Ⅰ）求证：EF⊥平面PBC；
（Ⅱ）求多面体PDFEC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网