题目内容
6.cos2($\frac{x}{2}$-$\frac{7}{8}$π)-cos2($\frac{x}{2}$+$\frac{7π}{8}$)可化简为( )| A. | $\sqrt{2}$sinx | B. | -$\sqrt{2}$sinx | C. | $\frac{\sqrt{2}}{2}$sinx | D. | -$\frac{\sqrt{2}}{2}$sinx |
分析 根据二倍角公式和两角和差的余弦公式化简计算即可.
解答 解:cos2($\frac{x}{2}$-$\frac{7}{8}$π)-cos2($\frac{x}{2}$+$\frac{7π}{8}$),
=$\frac{1}{2}$[1+cos(x-$\frac{7π}{4}$)]-$\frac{1}{2}$(1+cos(x+$\frac{7π}{4}$)],
=$\frac{1}{2}$[cos(x-$\frac{7π}{4}$)-cos(x+$\frac{7π}{4}$)],
=$\frac{1}{2}$(cosxcos$\frac{7π}{4}$+sinxsin$\frac{7π}{4}$-cosxcos$\frac{7π}{4}$+sinxsin$\frac{7π}{4}$),
=sinxsin$\frac{7π}{4}$,
=-sinxsin$\frac{π}{4}$,
=-$\frac{\sqrt{2}}{2}$sinx.
故选:D.
点评 本题考查了二倍角公式和两角和差的余弦公式,属于基础题.

练习册系列答案
相关题目
16.设向量$\overrightarrow{a}$=(2k+2,4),$\overrightarrow{b}$=(8,k+1),若$\overrightarrow{a}$,$\overrightarrow{b}$同向或反向,则k=( )
| A. | 3 | B. | -5 | C. | 0 | D. | 3或-5 |
16.已知$f(x)=\frac{sinx}{1+cosx}+1$,若$a=f(lg5),b=f(lg\frac{1}{5})$,则( )
| A. | a+b=0 | B. | a-b=0 | C. | a+b=2 | D. | a-b=2 |
17.为了得到$f(x)=2sin({3x-\frac{π}{3}})$的图象,只需将g(x)=2sinx的图象( )
| A. | 纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移$\frac{π}{9}$个单位 | |
| B. | 纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移$\frac{π}{3}$个单位 | |
| C. | 纵坐标不变,横坐标缩短为原来的$\frac{1}{3}$,再将所得图象向右平移$\frac{π}{3}$个单位 | |
| D. | 纵坐标不变,横坐标缩短为原来的$\frac{1}{3}$,再将所得图象向右平移$\frac{π}{9}$个单位 |
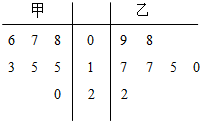 如图所示的茎叶图为甲、乙两家连锁店七天内销售额的某项指标统计:
如图所示的茎叶图为甲、乙两家连锁店七天内销售额的某项指标统计: