题目内容
形状如图所示的三个游戏盘中(图①是正方形,M,N分别是所在边中点,图②是半径分别为2和4的两个同心圆,O为圆心,图③是正六边形,点P为其中心)各有一个玻璃小球,依次摇动三个游戏盘后,将它们水平放置,就完成了一局游戏.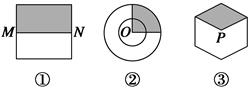
(1)一局游戏后,这三个盘中的小球都停在阴影部分的概率是多少?
(2)用随机变量X表示一局游戏后,小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值,求随机变量X的分布列.
(1) (2)X的分布列为
(2)X的分布列为X 1 3 P 

解析

练习册系列答案
相关题目
第17届亚运会将于2014年9月18日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
(1)根据调查数据制作2×2列联表;
(2)根据列联表的独立性检验,能否认为性别与喜爱运动有关?
| 参考数据 | 当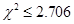 时,无充分证据判定变量 时,无充分证据判定变量 有关联,可以认为两变量无关联; 有关联,可以认为两变量无关联; |
当 时,有 时,有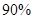 把握判定变量 把握判定变量 有关联; 有关联; | |
当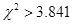 时,有 时,有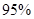 把握判定变量 把握判定变量 有关联; 有关联; | |
当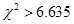 时,有 时,有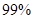 把握判定变量 把握判定变量 有关联. 有关联. |
 ,其中
,其中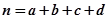 .)
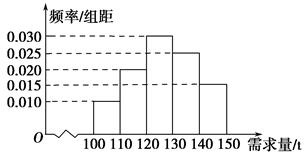
.) 为了提高食品的安全度,某食品安检部门调查了一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长速度(1.0~1.2 kg/年)的比例超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
| 鱼的 质量 | [1.00, 1.05) | [1.05, 1.10) | [1.10, 1.15) | [1.15, 1.20) | [1.20, 1.25) | [1.25, 1.30) |
| 鱼的 条数 | 3 | 20 | 35 | 31 | 9 | 2 |
(2)上面捕捞的100条鱼中间,从质量在[1.00,1.05)和[1.25,1.30)的鱼中,任取2条鱼来检测,求恰好所取得的鱼的质量在[1.00,1.05)和[1.25,1.30)各有1条的概率.
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
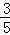 .
.(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为ξ,求ξ的分布列与期望.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
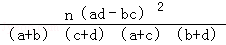 ,其中n=a+b+c+d)
,其中n=a+b+c+d) 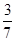 ,
,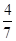 .
.