题目内容
为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
| 对别 | 北京 | 上海 | 天津 | 八一 |
| 人数 | 4 | 6 | 3 | 5 |
(Ⅱ)中国女排奋力拼搏,战胜了韩国队获得冠军,若要求选出两位队员代表发言,设其中来自北京队的人数为
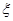 ,求随机变量
,求随机变量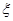 的分布列及数学期望
的分布列及数学期望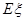
(Ⅰ)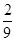 (Ⅱ)
(Ⅱ)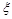 的分布列为:
的分布列为: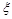
0 1 2 P 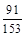
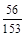
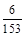
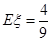 .
.
解析试题分析:(Ⅰ)从这18名队员中随机选出两名,求两人来自同一队的概率,本题是一个古典概型,试验发生包含的事件是这18名队员中随机选出两名,共有 种结果,满足条件的事件是两人来自于同一支球队,包括四种情况,表示出结果数,得到概率.(II)由题意知ξ的所有可能取值为0,1,2,结合变量对应的事件和古典概型的概率公式写出变量的概率,写出分布列,求出期望值.
种结果,满足条件的事件是两人来自于同一支球队,包括四种情况,表示出结果数,得到概率.(II)由题意知ξ的所有可能取值为0,1,2,结合变量对应的事件和古典概型的概率公式写出变量的概率,写出分布列,求出期望值.
试题解析:(Ⅰ)“从这18名队员中随机选出两名,两人来自于同一队”记作事件A,
则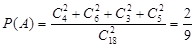 . (5分)
. (5分)
(Ⅱ)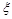 的所有可能取值为0,1,2. (7分)
的所有可能取值为0,1,2. (7分)
∵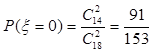 ,
,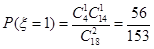 ,
,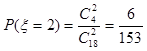 ,
,
∴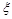 的分布列为:
的分布列为:
(10分)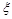
0 1 2 P 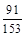
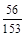
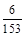
∴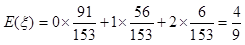 . (12分)
. (12分)
考点:离散型随机变量及其分布列;古典概型及其概率计算公式;离散型随机变量的期望与方差.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
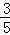 .
.(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为ξ,求ξ的分布列与期望.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
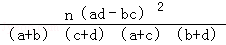 ,其中n=a+b+c+d)
,其中n=a+b+c+d) 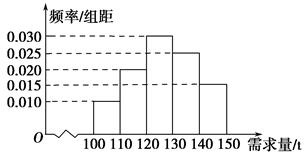
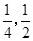 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为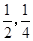 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.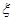 ,求
,求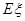 .
. 小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.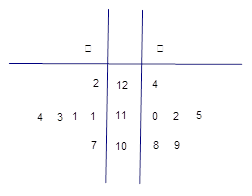
 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过 克的概率.
克的概率. 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求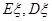 .
.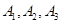 通晓日语,
通晓日语,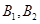 通晓俄语,
通晓俄语,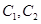 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.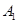 被选中的概率;(5分);(2)求
被选中的概率;(5分);(2)求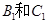 不全被选中的概率.(5分)
不全被选中的概率.(5分)