题目内容
设向量
，
满足|
+
|=
，|
-
|=
，则
•
=（ ）
| a |
| b |
| a |
| b |
| 15 |
| a |
| b |
| 11 |
| a |
| b |
| A、1 | B、2 | C、3 | D、5 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：采用平方法得|
+
|2-|
-
|2=15-11=4
•
，继而问题得以解决
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：∵|
+
|=
，|
-
|=
，
∴|
+
|2=15，|
-
|2=11，
∴|
+
|2-|
-
|2=15-11
∴4
•
=4，
∴
•
=1
故选：A
| a |
| b |
| 15 |
| a |
| b |
| 11 |
∴|
| a |
| b |
| a |
| b |
∴|
| a |
| b |
| a |
| b |
∴4
| a |
| b |
∴
| a |
| b |
故选：A
点评：本题主要考查了向量的混合运算，遇模一般采用平方，属于基础题
练习册系列答案
相关题目
过抛物线y2=4x的焦点F作两条互相垂直的直线l1，l2，l1交C于A、B，l2交C于M、N．则
+
=（ ）
| 1 |
| |AB| |
| 1 |
| |MN| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点A（2，1），抛物线y2=4x的焦点是F，若抛物线上存在一点P，使得|PA|+|PF|最小，则P点的坐标为（ ）
| A、（2，1） | ||
| B、（1，1） | ||
C、(
| ||
D、(
|
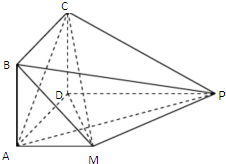如图，四边形ABCD是正方形，PD∥MA，MA⊥AD，PM⊥平面CDM，MA=AD=
如图，|