题目内容
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,O为坐标原点.若|AF|=3,求△AOB的面积.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据抛物线的定义方程求解得出:A(2,2
),即直线AF的方程为y=2
(x-1).
立直线与抛物线的方程
B(
,-
),运用S△AOB=
|OF|•|yA-yB|求解即可.
| 2 |
| 2 |
立直线与抛物线的方程
|
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
解答:
 解:如图所示,由题意知,抛物线的焦点F的坐标为(1,0),
解:如图所示,由题意知,抛物线的焦点F的坐标为(1,0),
又|AF|=3,由抛物线定义知:点A到准线x=-1的距离为3,
∴点A的横坐标为2.
将x=2代入y2=4x得y2=8,由图知点A的纵坐标y=2
,
∴A(2,2
),
∴直线AF的方程为y=2
(x-1).
联立直线与抛物线的方程
解之得
或
由图知B(
,-
),
∴S△AOB=
|OF|•|yA-yB|=
×1×|2
+
|=
.
 解:如图所示,由题意知,抛物线的焦点F的坐标为(1,0),
解:如图所示,由题意知,抛物线的焦点F的坐标为(1,0),又|AF|=3,由抛物线定义知:点A到准线x=-1的距离为3,
∴点A的横坐标为2.
将x=2代入y2=4x得y2=8,由图知点A的纵坐标y=2
| 2 |
∴A(2,2
| 2 |
∴直线AF的方程为y=2
| 2 |
联立直线与抛物线的方程
|
解之得
|
|
由图知B(
| 1 |
| 2 |
| 2 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
点评:本题考查了抛物线的几何性质,直线与抛物线的位置关系,运用方程组求解即可,属于中档题.

练习册系列答案
相关题目
设a,b,c为正数,a+b+9c2=1,则
+
+
c的最大值是( )
| a |
| b |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}满足an+2an=2an+1(n∈N*),且a1=1,a2=2,则数列{an}的前2014项的乘积为( )
| A、22012 |
| B、22013 |
| C、22014 |
| D、22015 |
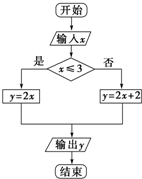 根据如图的框图回答后面的问题.
根据如图的框图回答后面的问题.