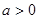题目内容
已知椭圆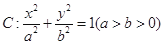 的离心率为
的离心率为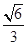 ,短轴一个端到右焦点的距离为
,短轴一个端到右焦点的距离为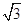 .
.
(Ⅰ)求椭圆C的方程:
(Ⅱ)设直线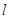 与椭圆C交于A、B两点,坐标原点O到直线
与椭圆C交于A、B两点,坐标原点O到直线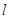 的距离为
的距离为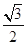 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
(Ⅰ) 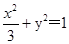 .
.
(Ⅱ) 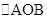 面积取最大值
面积取最大值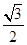 .
.
解析试题分析:(Ⅰ)属于椭圆的基本题型.通过建立 的方程组,求得椭圆方程为
的方程组,求得椭圆方程为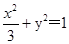 .
.
(Ⅱ)解答本小题,应注意讨论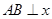 轴和当
轴和当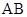 与
与 轴不垂直的两种情况.在
轴不垂直的两种情况.在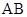 与
与 轴不垂直设直线
轴不垂直设直线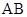 的方程为
的方程为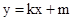 .利用坐标原点
.利用坐标原点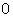 到直线
到直线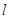 的距离为
的距离为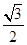 ,建立
,建立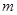 的方程.通过将直线方程与椭圆方程联立,应用韦达定理、弦长公式,得到
的方程.通过将直线方程与椭圆方程联立,应用韦达定理、弦长公式,得到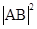 .应用均值定理得到
.应用均值定理得到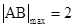 .
.
试题解析:(Ⅰ)设椭圆的半焦距为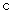 ,依题意,离心率为
,依题意,离心率为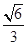 ,短轴一个端到右焦点的距离为
,短轴一个端到右焦点的距离为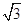 .
.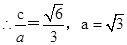 ,
,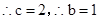 ,∴所求椭圆方程为
,∴所求椭圆方程为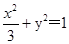 .
.
(Ⅱ)设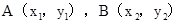 .
.
①当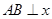 轴时,
轴时,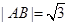 .
.
②当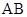 与
与 轴不垂直时,设直线
轴不垂直时,设直线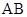 的方程为
的方程为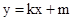 .
.
∵坐标原点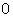 到直线
到直线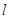 的距离为
的距离为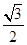 ,
,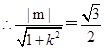 ,
,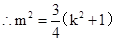
把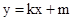 代入椭圆方程,整理得
代入椭圆方程,整理得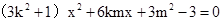 ,
,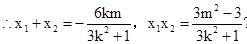
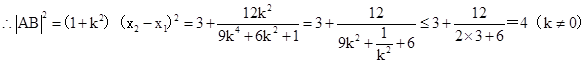
当且仅当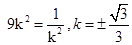 时等号成立,
时等号成立,
当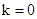 时,
时,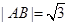 ,
,
综上所述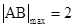 .
.
∴当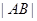 最大时,
最大时, 面积取最大值
面积取最大值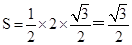 .
.
考点:椭圆方程,直线与椭圆的位置关系,均值定理的应用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
若对任意x∈R,不等式|x|≥ax恒成立,则实数a的取值范围是( )
| A.a<-1 | B.|a|≤1 | C.|a|<1 | D.a≥1 |
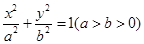 的右准线
的右准线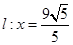 ,离心率
,离心率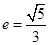 ,
, ,
, 是椭圆上的两动点,动点
是椭圆上的两动点,动点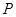 满足
满足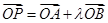 ,(其中
,(其中 为常数).
为常数).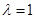 且直线
且直线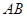 与
与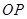 斜率均存在时,求
斜率均存在时,求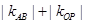 的最小值;
的最小值;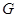 是线段
是线段 ,问是否存在常数
,问是否存在常数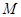 ,
,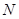 ,使得动点
,使得动点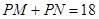 ,若存在,求出
,若存在,求出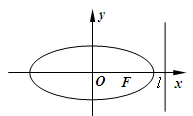
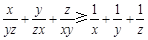 .
. 的三段式污水处理池,池高为1
的三段式污水处理池,池高为1 ,如果池的四周墙壁的建造费单价为
,如果池的四周墙壁的建造费单价为 元
元 ,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为
,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为 元
元 元
元 ,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元? ,
, 及
及 的符号;
的符号; ”.
”. 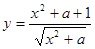 的最小值,其中
的最小值,其中