题目内容
某工厂拟建一座平面图为矩形,面积为 的三段式污水处理池,池高为1
的三段式污水处理池,池高为1 ,如果池的四周墙壁的建造费单价为
,如果池的四周墙壁的建造费单价为 元
元 ,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为
,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为 元
元 ,池底的建造费单价为
,池底的建造费单价为 元
元 ,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?
污水池的长宽分别为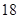
 ,
,  时造价最低,为
时造价最低,为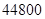 元.
元.
解析试题分析:设污水池的宽为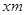 ,则长为
,则长为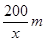 ,水池的造价为
,水池的造价为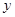 元,则由题意知:定义域为
元,则由题意知:定义域为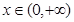 ,
,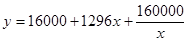 ,利用基本不等式即可求得其最值.
,利用基本不等式即可求得其最值.
试题解析:
设污水池的宽为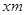 ,则长为
,则长为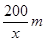 ,水池的造价为
,水池的造价为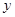 元,则由题意知:定义域为
元,则由题意知:定义域为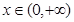 ,
,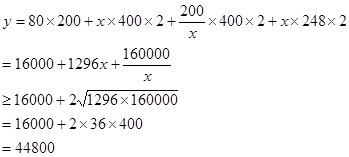
当且仅当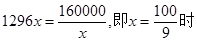 ,取“=”,
,取“=”,
此时长为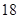
 ,即污水池的长宽分别为
,即污水池的长宽分别为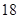
 ,
,  时造价最低,为
时造价最低,为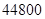 元.
元.
考点:本题考查了基本不等式的应用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
若点(x, y)位于曲线y =" |x|" 与y = 2所围成的封闭区域, 则2x-y的最小值为( )
| A.-2 | B.-6 | C.0 | D.2 |
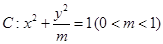 的左顶点为
的左顶点为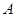 ,
,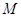 是椭圆
是椭圆 上异于点
上异于点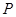 与点
与点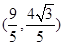 ,求
,求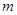 的值;
的值;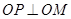 ,求
,求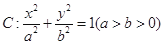 的离心率为
的离心率为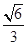 ,短轴一个端到右焦点的距离为
,短轴一个端到右焦点的距离为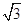 .
.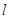 与椭圆C交于A、B两点,坐标原点O到直线
与椭圆C交于A、B两点,坐标原点O到直线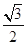 ,求△AOB面积的最大值.
,求△AOB面积的最大值.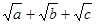 的最大值.
的最大值.
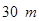 ,则这个矩形的长,宽各为多少时,菜园的面积最大?
,则这个矩形的长,宽各为多少时,菜园的面积最大?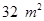 ,则这个矩形的长,宽各为多少时,篱笆的总长最短?
,则这个矩形的长,宽各为多少时,篱笆的总长最短?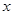 万件与投入技术改革费用
万件与投入技术改革费用 万元(
万元( )满足
)满足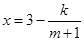 (
(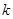 为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的
为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的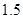 倍(生产成本包括固定投入和再投入两部分资金).
倍(生产成本包括固定投入和再投入两部分资金). 万元表示为技术改革费用
万元表示为技术改革费用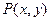 在直线
在直线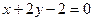 上,则
上,则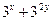 的最小值是.
的最小值是. ,x∈[1,+∞).
,x∈[1,+∞).