题目内容
若对任意x∈R,不等式|x|≥ax恒成立,则实数a的取值范围是( )
| A.a<-1 | B.|a|≤1 | C.|a|<1 | D.a≥1 |
B
解析试题分析:当x=0时,显然无论a为何值,不等式|x|≥ax总恒成立;当x>0时,不等式|x|≥ax恒成立等价于: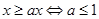 ;当x<0时,不等式|x|≥ax恒成立等价于:
;当x<0时,不等式|x|≥ax恒成立等价于: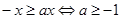 ;所以对任意x∈R,不等式|x|≥ax恒成立,有
;所以对任意x∈R,不等式|x|≥ax恒成立,有 ;故选B.
;故选B.
另解:对任意x∈R,不等式|x|≥ax恒成立,等价于函数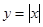 的图象恒在直线
的图象恒在直线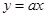 的上方,如图:
的上方,如图: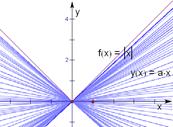
可知必须且只需 ;故选B.
;故选B.
考点:不等式的恒成立.

练习册系列答案
相关题目
设 在约束条件
在约束条件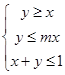 下,目标函数
下,目标函数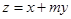 的最大值大于2,则
的最大值大于2,则 的取值范围为( ).
的取值范围为( ).
A.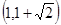 | B. | C.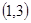 | D.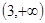 |
若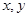 满足
满足 且
且 的最小值为-4,则
的最小值为-4,则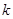 的值为( )
的值为( )
A.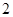 | B.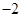 | C.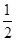 | D.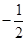 |
若点(x, y)位于曲线y =" |x|" 与y = 2所围成的封闭区域, 则2x-y的最小值为( )
| A.-2 | B.-6 | C.0 | D.2 |
设实数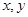 满足约束条件
满足约束条件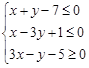 ,则
,则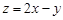 的最大值为( )
的最大值为( )
| A.10 | B.8 | C.3 | D.2 |
若变量 、
、 满足约束条件
满足约束条件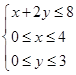 ,则
,则 的最大值等于( )
的最大值等于( )
A. | B.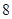 | C. | D. |
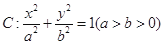 的离心率为
的离心率为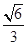 ,短轴一个端到右焦点的距离为
,短轴一个端到右焦点的距离为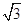 .
.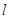 与椭圆C交于A、B两点,坐标原点O到直线
与椭圆C交于A、B两点,坐标原点O到直线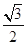 ,求△AOB面积的最大值.
,求△AOB面积的最大值.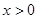 ,求函数
,求函数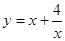 的最小值,并求此时x的值.
的最小值,并求此时x的值.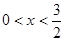 ,求函数
,求函数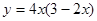 的最大值.
的最大值.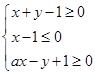 (a为常数)所表示的平面区域的面积等于2,则a的值为( )
(a为常数)所表示的平面区域的面积等于2,则a的值为( )