题目内容
已知函数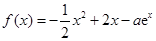 .
.
(1)若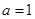 ,求
,求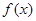 在
在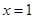 处的切线方程;
处的切线方程;
(2)若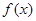 在
在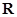 上是增函数,求实数
上是增函数,求实数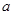 的取值范围.
的取值范围.
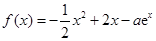 .
.(1)若
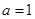 ,求
,求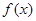 在
在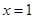 处的切线方程;
处的切线方程;(2)若
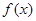 在
在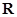 上是增函数,求实数
上是增函数,求实数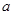 的取值范围.
的取值范围.(1)故曲线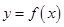 在
在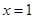 处的切线方程为
处的切线方程为 ;(2)
;(2) .
.
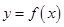 在
在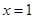 处的切线方程为
处的切线方程为 ;(2)
;(2) .
.试题分析:(1)先将
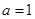 代入函数
代入函数 的解析式,并求出导数
的解析式,并求出导数 ,然后分别求出
,然后分别求出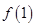 与
与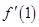 的值,最后利用点斜式求出切线方程;(2)将“函数
的值,最后利用点斜式求出切线方程;(2)将“函数 在
在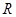 上是增函数”这一条件转化为“不等式
上是增函数”这一条件转化为“不等式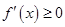 在
在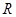 上恒成立”进行求解,结合参数分离法转化为“不等式
上恒成立”进行求解,结合参数分离法转化为“不等式 在
在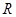 上恒成立”型不等式进行处理,即等价于“
上恒成立”型不等式进行处理,即等价于“ ”,最后利用导数求出函数
”,最后利用导数求出函数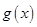 在
在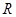 上的最小值,从而得到参数
上的最小值,从而得到参数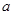 的取值范围.
的取值范围.试题解析:(1)当
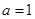 时,
时,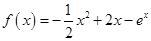 ,则
,则 ,
,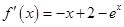 ,
, ,
,故曲线
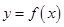 在
在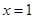 处的切线方程为
处的切线方程为 ,即
,即 ;
;(2)
 在
在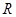 上是增函数,则
上是增函数,则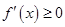 上恒成立,
上恒成立,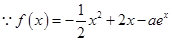 ,
, ,
,于是有不等式
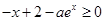 在
在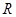 上恒成立,即
上恒成立,即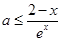 在
在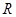 上恒成立,
上恒成立,令
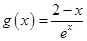 ,则
,则 ,令
,令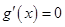 ,解得
,解得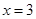 ,列表如下:
,列表如下: |  |  | 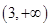 |
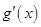 |  |  | 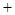 |
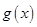 | 减 | 极小值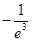 | 增 |
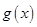 在
在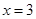 处取得极小值,亦即最小值,即
处取得极小值,亦即最小值,即 ,所以
,所以 ,
,即实数
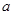 的取值范围是
的取值范围是 .
.
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
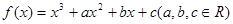 的图像过原点,且在
的图像过原点,且在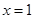 处的切线为直线
处的切线为直线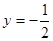
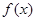 的解析式;
的解析式;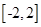 上的最小值和最大值.
上的最小值和最大值.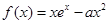 .
.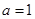 时,求
时,求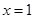 处的切线方程;
处的切线方程;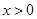 时,
时,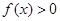 ,求
,求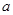 的取值范围.
的取值范围. .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值; 的单调区间.
的单调区间.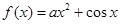 .
.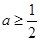 时,函数
时,函数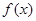 在
在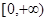 上单调递增;
上单调递增;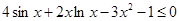 .
.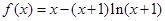 (
(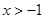 ).
).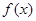 的单调区间;
的单调区间;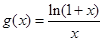 (
(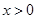 )的单调性证明:当
)的单调性证明:当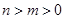 时,
时,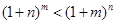 ;
;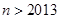 ,且
,且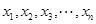 均为正实数,
均为正实数, 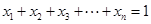 时,
时,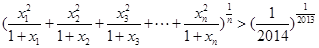 .
.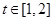 ,函数
,函数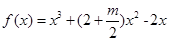 在区间
在区间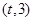 上总不是单调函数,求
上总不是单调函数,求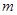 的取值范围是( )
的取值范围是( )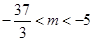
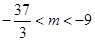
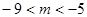
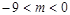
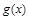 为三次函数
为三次函数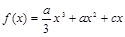 的导函数,则函数
的导函数,则函数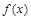 的图像可能是( )
的图像可能是( )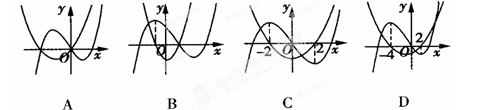
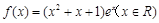 的单调减区间为
的单调减区间为