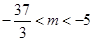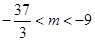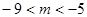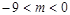题目内容
已知函数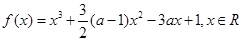 .
.
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)当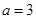 时,若函数
时,若函数 在区间
在区间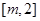 上的最大值为28,求
上的最大值为28,求 的取值范围.
的取值范围.
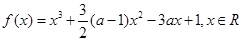 .
.(Ⅰ)讨论函数
 的单调区间;
的单调区间;(Ⅱ)当
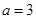 时,若函数
时,若函数 在区间
在区间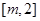 上的最大值为28,求
上的最大值为28,求 的取值范围.
的取值范围.(Ⅰ)当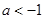 时,
时, 在
在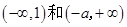 内单调递增,
内单调递增, 在
在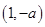 内单调递减;当
内单调递减;当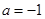 时,
时, 在
在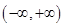 单调递增;当
单调递增;当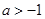 时,
时, 在
在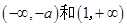 内单调递增,
内单调递增, 在
在 内单调递减;(Ⅱ)即
内单调递减;(Ⅱ)即 的取值范围是
的取值范围是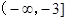 .
.
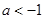 时,
时, 在
在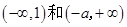 内单调递增,
内单调递增, 在
在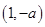 内单调递减;当
内单调递减;当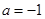 时,
时, 在
在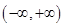 单调递增;当
单调递增;当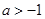 时,
时, 在
在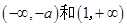 内单调递增,
内单调递增, 在
在 内单调递减;(Ⅱ)即
内单调递减;(Ⅱ)即 的取值范围是
的取值范围是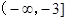 .
.试题分析:(Ⅰ)讨论函数
 的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出
的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出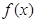 的导函数,判断
的导函数,判断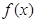 的导函数的符号,从而求出
的导函数的符号,从而求出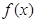 的单调区间;但本题求导后令
的单调区间;但本题求导后令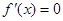 ,得
,得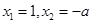 ,由于不知
,由于不知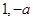 的大小,因此需要对
的大小,因此需要对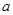 进行分类讨论,从而确定在各种情况下的单调区间;(Ⅱ)当
进行分类讨论,从而确定在各种情况下的单调区间;(Ⅱ)当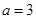 时,若函数
时,若函数 在区间
在区间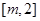 上的最大值为28,求
上的最大值为28,求 的取值范围,这是函数在闭区间上的最值问题,像这一类问题的处理方法为,先求出
的取值范围,这是函数在闭区间上的最值问题,像这一类问题的处理方法为,先求出 的极值点,然后分别求出极值点与区间端点处的函数值,比较谁大谁为最大值,比较谁小谁为最小值,但本题是给出最大值,确定区间端点的取值范围,只需找出包含最大值28的
的极值点,然后分别求出极值点与区间端点处的函数值,比较谁大谁为最大值,比较谁小谁为最小值,但本题是给出最大值,确定区间端点的取值范围,只需找出包含最大值28的 的取值范围,
的取值范围,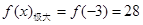 ,故故区间
,故故区间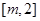 内必须含有
内必须含有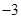 ,即
,即 的取值范围是
的取值范围是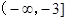 .
.试题解析:(Ⅰ)
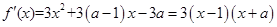 ,令
,令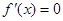 得
得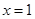 ,
,(ⅰ)当
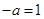 ,即
,即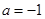 时,
时, ,
, 在
在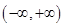 单调递增,
单调递增,(ⅱ)当
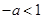 ,即
,即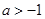 时,当
时,当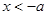 ,或
,或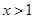 时,
时,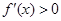 ,
, 在
在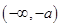 、
、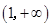 内单调递增,当
内单调递增,当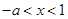 时
时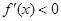 ,
, 在
在 内单调递减,
内单调递减,(ⅲ)当
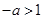 ,即
,即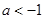 时,当
时,当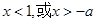 时
时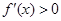 ,
, 在
在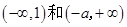 内单调递增
内单调递增当
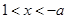 时
时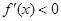 ,
, 在
在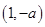 内单调递减 ,
内单调递减 ,综上,当
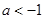 时,
时, 在
在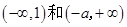 内单调递增,
内单调递增, 在
在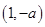 内单调递减;当
内单调递减;当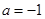 时,
时, 在
在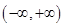 单调递增;当
单调递增;当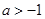 时,
时, 在
在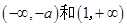 内单调递增,
内单调递增, 在
在 内单调递减;
内单调递减;(Ⅱ)当
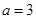 时,
时,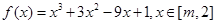 ,
,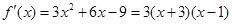 ,令
,令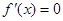 得
得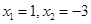 ,将
,将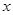 ,
,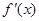 ,
, 变化情况列表如下:
变化情况列表如下: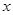 | 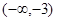 | 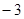 | 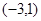 | 1 | 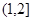 |
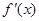 | 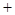 | 0 | 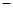 | 0 | 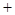 |
 | ↗ | 极大 | ↘ | 极小 | ↗ |
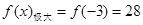 ,
,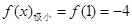 ,
,又
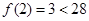 ,故区间
,故区间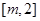 内必须含有
内必须含有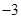 ,即
,即 的取值范围是
的取值范围是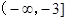 .
.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 .
. 的值域为
的值域为 .求关于
.求关于 的不等式
的不等式 的解集;
的解集; 时,
时, 为常数,且
为常数,且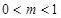 ,
,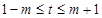 ,求
,求 的最小值.
的最小值. (
(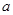 ≠0,
≠0, ,求函数
,求函数 的极值和单调区间;
的极值和单调区间; ,使得
,使得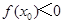 成立,求实数
成立,求实数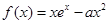 .
.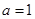 时,求
时,求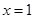 处的切线方程;
处的切线方程;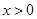 时,
时,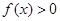 ,求
,求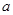 的取值范围.
的取值范围. .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值; 的单调区间.
的单调区间.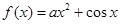 .
.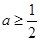 时,函数
时,函数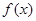 在
在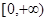 上单调递增;
上单调递增;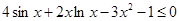 .
.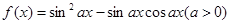 的图象与直线
的图象与直线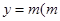 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为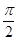
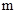 的值;
的值; 是
是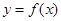 图象的对称中心,且
图象的对称中心,且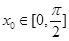 ,求点A的坐标
,求点A的坐标 的图象在
的图象在 处的切线与圆
处的切线与圆 相切,则
相切,则 的最大值是( )
的最大值是( )

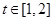 ,函数
,函数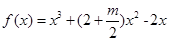 在区间
在区间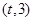 上总不是单调函数,求
上总不是单调函数,求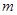 的取值范围是( )
的取值范围是( )