题目内容
过双曲线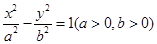 的一个焦点F作一条渐近线的垂线,若垂足恰在线段
的一个焦点F作一条渐近线的垂线,若垂足恰在线段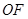 (
( 为原点)的垂直平分线上,则双曲线的离心率为 .
为原点)的垂直平分线上,则双曲线的离心率为 .

解析试题分析:不妨设从右焦点 向其中的一条渐近线
向其中的一条渐近线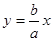 作垂线,垂足为
作垂线,垂足为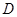 ,因为垂足恰在线段
,因为垂足恰在线段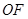 的垂直平分线上,根据直角三角形斜边上的中线等于斜边的一半可知点
的垂直平分线上,根据直角三角形斜边上的中线等于斜边的一半可知点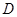 坐标为
坐标为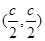 ,代入渐近线
,代入渐近线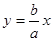 ,可得
,可得
考点:本小题主要考查双曲线中基本量的关系和离心率的求法,考查学生数形结合思想的应用和运算求解能力.
点评:解决本小题的关键在于根据直角三角形斜边上的中线等于斜边的一半得出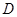 的坐标,如果换成其余求
的坐标,如果换成其余求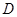 的坐标的方法,可能计算量会大很多.
的坐标的方法,可能计算量会大很多.

练习册系列答案
相关题目
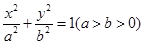 ,
,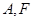 是其左顶点和左焦点,
是其左顶点和左焦点, 是圆
是圆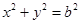 上的动点,若
上的动点,若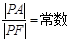 ,则此椭圆的离心率是
,则此椭圆的离心率是 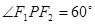 ,
,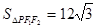 .该双曲线的标准方程为
.该双曲线的标准方程为 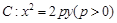 上一点
上一点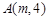 到其焦点的距离为
到其焦点的距离为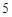 ,则m= .
,则m= .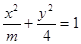 的离心率为
的离心率为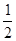 ,则
,则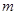 为 .
为 .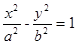 (a>0,b>0)上,C的焦距为4,则它的离心率为_____________.
(a>0,b>0)上,C的焦距为4,则它的离心率为_____________.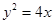 上一点
上一点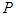 引抛物线准线的垂线,垂足为
引抛物线准线的垂线,垂足为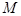 ,且
,且 ,设抛物线的焦点为
,设抛物线的焦点为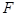 ,则
,则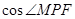 = .
= .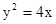 的焦点,与抛物线交与A、B两点,则
的焦点,与抛物线交与A、B两点,则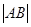 = .
= .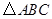 中,
中, .若以
.若以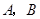 为焦点的椭圆经过点
为焦点的椭圆经过点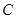 ,则该椭圆的离心率
,则该椭圆的离心率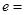 .
.