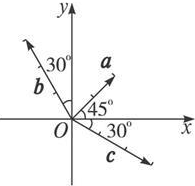
题目内容
14．如图，在正三棱柱中，E是AC中点，求证：AB′∥面BEC′．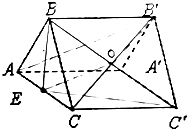
分析 连接B′C交BC′于点O，连接EO，则O为B′C的中点，根据E是AC中点，可得EO∥AB′，从而可证AB′∥平面BEC′；
解答 证明：连接B′C交BC′于点O，连接EO，则O为B′C的中点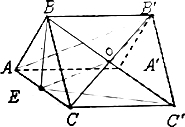
∵E是AC中点，
∴EO∥AB′，
∵AB′?平面BEC′，EO?平面BEC′，
∴AB′∥平面BEC′；
点评 本题考查的知识点是直线与平面平行的判定，熟练掌握线面平行的判定定理是解答的关键．
练习册系列答案
相关题目
6．已知A1、A2是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左右顶点，双曲线C的焦距为2c，P为右支上异于A2的一点，直线PA2与直线x=$\frac{{a}^{2}}{c}$相交于点Q，若$\overrightarrow{{A}_{1}P}$•$\overrightarrow{{A}_{1}Q}$=0，则双曲线C的渐近线方程为（ ）
| A． | y=±2x | B． | y=±x | C． | y=±$\sqrt{3}$x | D． | y=±$\frac{\sqrt{3}}{3}$x |
3．
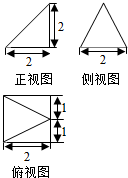已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（ ）cm2．
已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（ ）cm2．| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 2 | D． | 4 |
4．直线3x-$\sqrt{3}y$+1=0的倾斜角为（ ）
| A． | 120° | B． | 90° | C． | 60° | D． | 30° |